Ressenti du relief et du volume, le cerveau, l'anaglyphe :
Pour recréer du volume, le cerveau a besoin de deux images prises depuis deux points espacés d'une distance appelée la base stéréo. Nos deux yeux sont espacés d'environ 6,5 à 7 cm. Cette base entre les deux images obtenues par chaque œil introduit une parallaxe de vision -décalage angulaire horizontal- qui suffit au cerveau pour apprécier des différences de distances et le volume jusqu'à environ 2 km dans les meilleures conditions en comparaison.
Un procédé de restitution du relief parfait doit donc pouvoir injecter dans le cerveau les deux images identiques à la scène, sans ambigüité, sans les tronquer, sans leur enlever une partie ou une caractéristique.
Le procédé de restitution du relief le plus connu du grand public est sans doute l'anaglyphe. Il est le plus simple et le plus facilement diffusable en masse à bas coût car il suffit d'une image informatique et d'une paire de lunettes à filtres colorés pour pouvoir faire apprécier une scène en relief. Mais par nature, il n'est pas le plus adapté à la photographie en couleur, la meilleure restitution du relief.
En effet, le procédé anaglyptique "code" le relief par des couleurs complémentaires (le plus souvent rouge et cyan). Un anaglyphe est en fait simplement la composante rouge de l'image de gauche à laquelle on ajoute la composante cyan (vert+bleu) de l'image de droite. Avec des lunettes disposants d'un filtre rouge (devant l'œil gauche) et d'un filtre cyan (devant l'œil droit), on injecte alors dans le cerveau les deux images filtrées correspondantes à l'œil gauche et l'œil droit -qui sont décalées d'une parallaxe horizontale, d'un angle de vision-. En fait, il s'agit de la composante rouge de l'anaglyphe -originaire image de gauche- (elle traverse le filtre rouge, mais pas le filtre cyan) qui est injectée dans l'œil gauche, et la composante cyan de l'anaglyphe -originaire image de droite- (elle traverse le filtre cyan, mais pas le filtre rouge) qui est injectée dans l'œil droit. Le cerveau recombine/fusionne le tout et recrée une sensation de relief et de profondeur en associant les informations de position reçues simultanément PAR LES DEUX yeux -on parle ici de stéréovision, stéréoscopie-.
Cette dernière remarque est très importante car elle met en avant le problème majeur du procédé anaglyptique. C'est à dire que pour des objets de la scène de couleurs identiques aux filtres utilisés, l'information de position ne peut passer que dans un SEUL œil. Par exemple, imaginons un objet rouge pur dans un anaglyphe utilisant les complémentaires filtrantes rouge/cyan, cet objet ne sera forcément perçu QUE par l'œil gauche puisque aucune information lumineuse émanant de lui NE pourra traverser le filtre cyan. Idem pour un objet cyan, il ne sera perçu QUE par l'œil droit puisque le cyan (vert+bleu) ne peut pas traverser un filtre rouge. Ces deux couleurs ne sont pas des "couleurs stéréoscopiques" pour un anaglyphe rouge/cyan. (En pratique c'est plus compliqué car les filtres des lunettes et les sources des écrans ne sont pas purs, d'où problèmes de diaphotie).
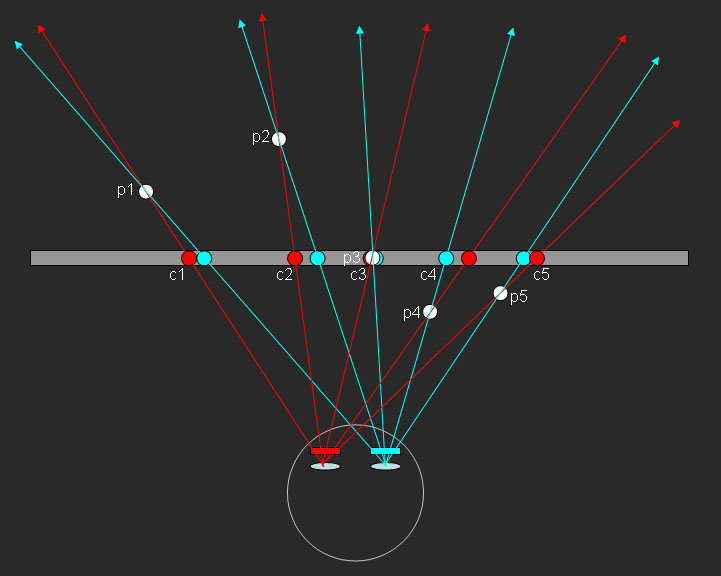
Illustration : formation de la profondeur / relief / volume dans l'espace par un anaglyphe. Le plan horizontal gris est le plan de l'anaglyphe. Un point dans l'espace est situé par un couple dans sa couche rouge et dans sa couche cyan. Le cerveau place le point dans l'espace à l'intersection des segments partant des yeux et passant par ces points associés. La distance et "l'ordre" entre le détail dans la composante rouge et la composante cyan fixent la profondeur. Dans cet exemple, les couples Cn sont situés en Pn. S'il manque une des deux composantes, le cerveau n'a plus l'information de la parallaxe horizontale. Il doit interpréter cérébralement ce qui n'est pas évident selon la scène.
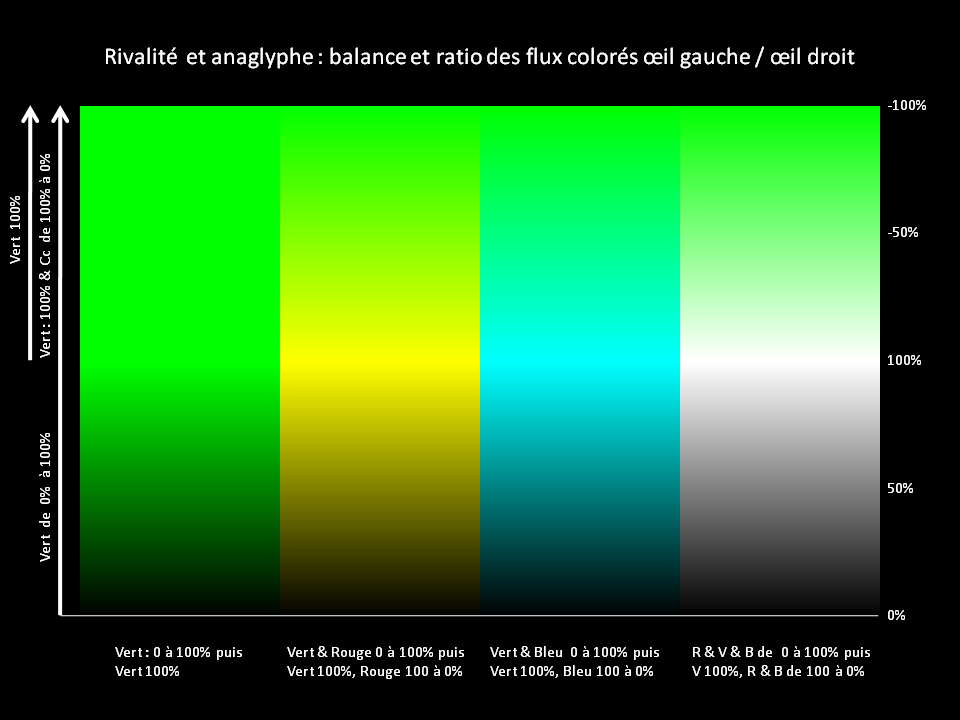
Le cerveau ne reçoit donc pour cet objet coloré que l'information de position par un seul œil. Il voit l'objet très lumineux d'un œil et quasi noir de l'autre. Il est hésitant entre la donnée angulaire qu'il N'A PAS FORCEMENT et l'interprétation cérébrale qu'il tente de faire avec les objets environnants sur les bordures et contours. Il est ébloui par un œil et pas l'autre, fort contraste entre les deux yeux. C'est un peu comme si on ne fermait un œil QUE pour cet objet de la scène... Cet objet est perçu comme une hésitation, il vibre dans l'image, sa vision est désagréable et pas stable... On dit qu'il y a une rivalité de couleur. Ce mécanisme de rivalité colorée n'est pas binaire, c'est à dire qu'il y a toute une gradation du problème avec des couleurs qui ne vibrent pas complètement mais qui gêne à la bonne vision du relief, à la bonne appréciation de la profondeur. Dans les trois illustrations qui suivent de fortes et faibles rivalités de couleurs sont présentes graduellement. Il faut les regarder attentivement avec les lunettes chaussées. Vous allez percevoir une sensation désagréable sur les zones où un œil reçoit beaucoup plus de flux lumineux que sur l'autre. En revanche, les zones où il y a un équilibre satisfaisant entre le flux lumineux sur les deux yeux sont perçues sans aucune gêne, ce sont les "couleurs stéréoscopiques" pour l'anaglyphe. Il est intéressant :
- d'observer ces illustrations avec différentes lunettes (pour anaglyphes rouge/cyan) pour s'apercevoir que l'aspect et l'effet est très dépendant des filtres des lunettes. C'est parfois épouvantable avec certaines lunettes qui disposent de filtres assez purs. En fait l'effet et la gêne dépend du couple écran/lunette pureté/diaphotie ;
- vous remarquerez que les zones de fortes rivalités sont difficilement situables sur l'axe de la profondeur. En fait on hésite constamment, l'image vibre. L'effet n'est pas binaire, il y a une gradation dans l'intensité du problème de la rivalité colorée ;
- une teinte unie pure est rapidement désagréable à partir d'un déséquilibre de flux de 25% entre les deux yeux. Mais la sensation de vraiment désagréable pas au même ratio selon la teinte nuancée (plus désagréable avec les rouges qu'avec les bleus) ;
- il est intéressant de faire passer la souris (curseur BLANC, donc un détail situé sans ambigüité en profondeur sur la surface de l'écran) sur les différentes zones du graphique -en observant avec les lunettes-. Parfois sur certaines zones la souris vibre autant. Elle peut devenir difficile à situer en profondeur, l'objet souris n'est pas situé clairement et uniquement par les bordures/contours de sa forme, un autre mécanisme le contrarie. Parfois on arrive à la situer correctement sur l'écran selon la couleur environnante. Les couleurs rivales participent donc à la destruction de la bonne perception de la profondeur dans un anaglyphe, le rendant graduellement incohérent sur certaines zones pour le cerveau examinateur.
Variations sur les nuances de ROUGE maxi -œil gauche -
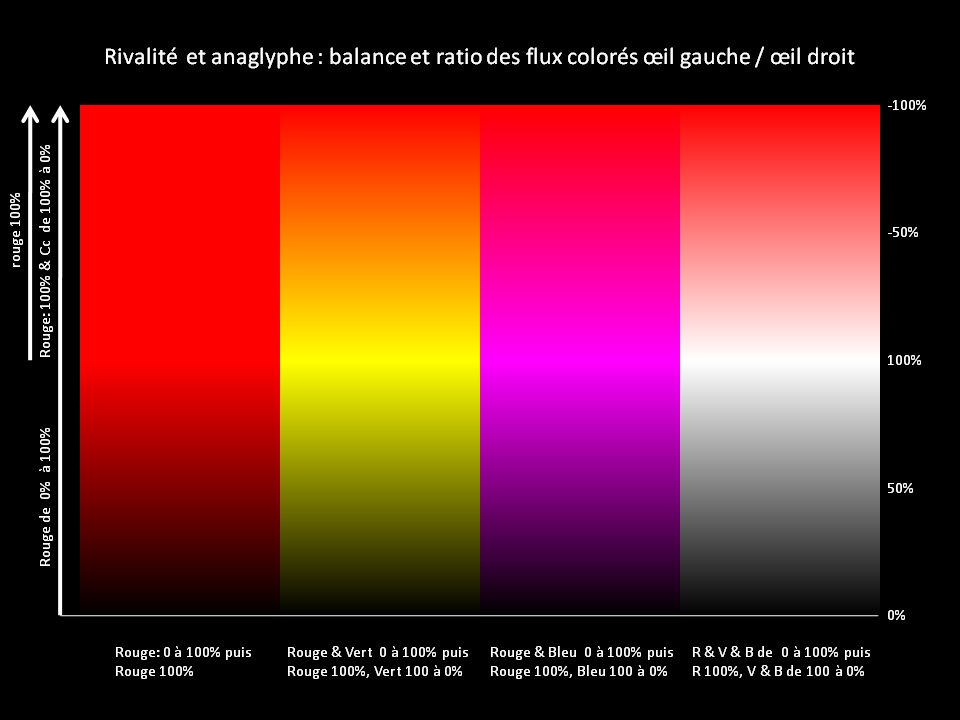
Variations sur les nuances de VERT maxi - œil droit -
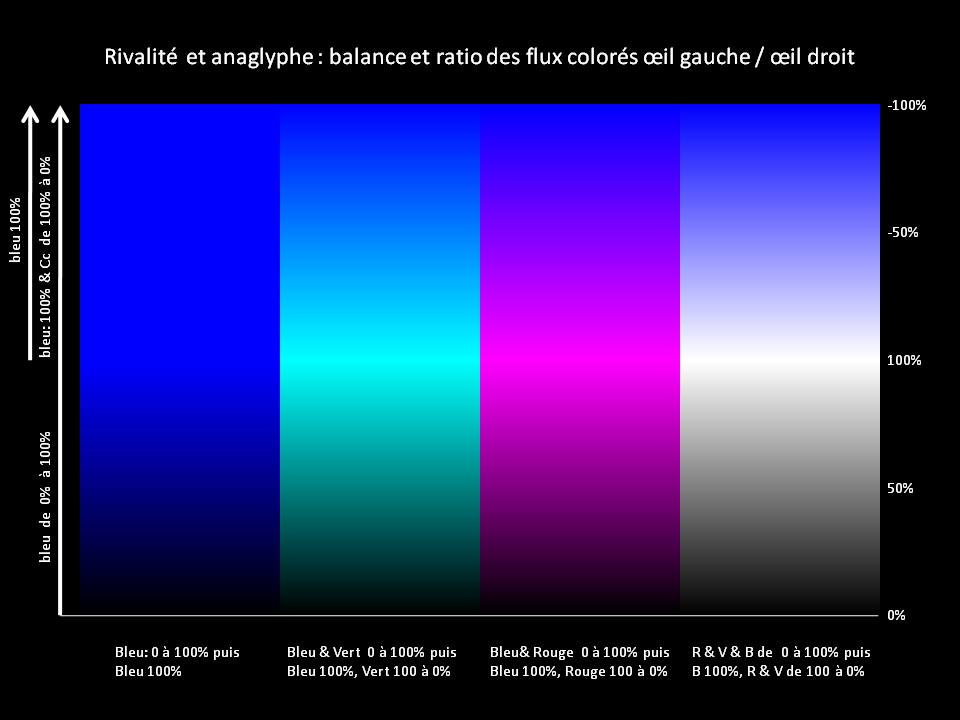
Variations sur les nuances de BLEU maxi - œil droit -
Pour contrer ces problèmes induits par le procédé, il faut donc adapter les couleurs originales des objets des images du couple stéréophotographique au procédé anaglyptique en les transformant en des couleurs proches mais qui passent aussi bien dans le filtre rouge que le filtre cyan de manière à fournir une information satisfaisante et cohérente au cerveau comme en vision naturelle non perturbée par une "maladie".
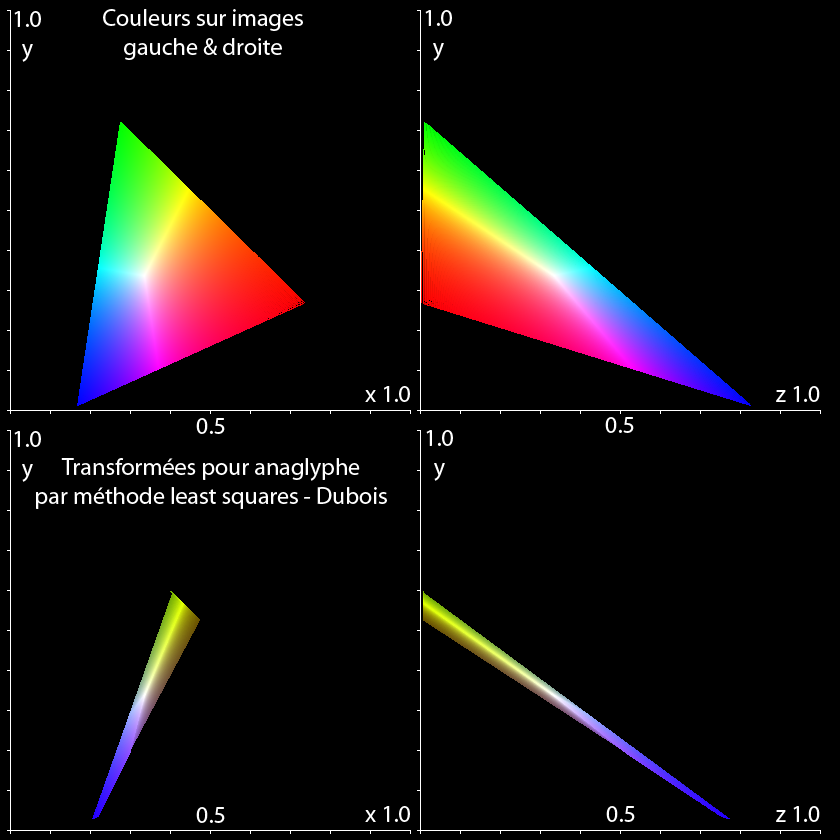
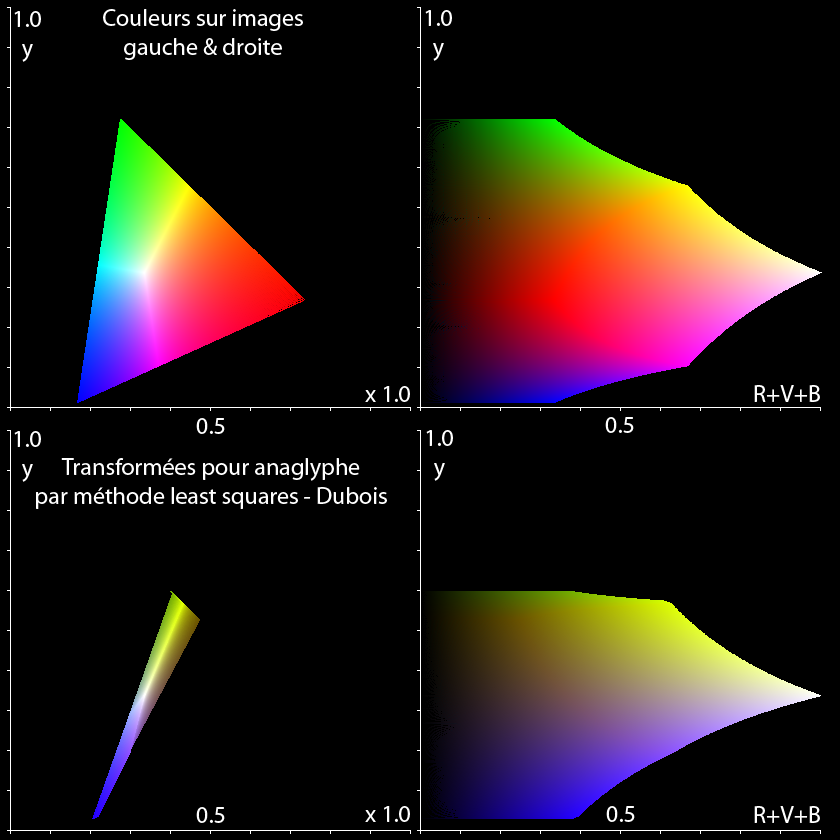
Eric DUBOIS, chercheur Canadien de la "School of Information Technology and Engineering, University of Ottawa, Ontario, Canada" a proposé une méthode mathématique complète tenant compte du spectre d'absorption des filtres des lunettes (type Roscolux #25 et #69 dans son application numérique), de la densité spectrale des sources primaires des écrans d'ordinateur (CRT Sony Trinitron), et de la sensibilité spectrale de l'œil humain. Cette méthode rigoureuse et astucieuse décrite dans son article "A projection method to generate anaglyph stereo images" 0-7803-7041-4/01 IEEE 2001" permet d'adapter les couleurs originales de pixels homologues du couple (en correspondance dans les deux images gauche et droite) vers la création de la couleur du pixel correspondant dans un anaglyphe. La couleur ainsi obtenue est la plus proche possible de l'originale, en minimisant les distances entre les deux couleurs dans le diagramme colorimétrique CIE par projection via les moindres carrés. Elle permet de calculer la transformation adéquate pour passer d'un espace de couleurs original vers un sous ensemble de couleurs qui s'en approche le plus à travers le couple écran-lunette et l'œil humain standard.
Les couleurs obtenues ne sont plus tout à fait les originales surtout pour les objets rouges et cyans mais la plupart du temps elles ne sont pas choquantes. Les personnages sont par exemple un peu plus jaunes-vert que naturel, le coucher de soleil devient plus verdâtre, le bleu du ciel passe du cyan à plus bleu... L'image est généralement un peu plus sombre et la transformation ne préserve pas l'égalité des couleurs. Les gris sont conservés ainsi que le blanc. Il faut choisir entre le confort de vision et le réalisme... Les couleurs obtenues sont plus stéréoscopiques.
Le lecteur familier du formalisme mathématique et l'abstraction se rapportera à cette référence. Dans les lignes qui suivent nous essayerons d'expliquer par l'exemple numérique et schématique les conséquences et l'action de cette transformation. Pourquoi la vision de l'anaglyphe est plus confortable ?
Les études réalisées par Eric Dubois conduisent au calcul des membres d'une matrice dont les valeurs sont fonctions des caractéristiques des filtres des lunettes et sources primaires des écrans. Il suffit de multiplier cette matrice par les valeurs RVB (doses rouges vertes et bleues, la couleur codée par les trois primaires quantifiées de la synthèse additive) des pixels homologues dans les images gauche et droite pour obtenir les valeurs RVB -la couleur- associée dans l'anaglyphe résultant.
Dans "A uniform metric for anaglyph computation", Zhe Zhang et David F. Mc Allister de l'Université de Caroline du Nord (USA) donnent les valeurs des membres de la matrice de transformation ci-dessous. Ces valeurs correspondent aux sources primaires d'un moniteur LCD standard et des filtres des lunettes type 5450C.

Qui se calcule directement pour chaque composantes RVB du pixel de l'anaglyphe avec les pixels homologues associés du couple stéréo par :
Dose Rouge pixel anaglyphe = Dose Rouge pixel image gauche * 0.4154 + Dose Verte pixel image gauche * 0.4710 + Dose Bleue pixel image gauche * 0.1669 + Dose Rouge pixel image droite * -0.0109 + Dose Verte pixel image droite * -0.0364 + Dose Bleue pixel image droite * -0.0060
Dose Verte pixel anaglyphe = Dose Rouge pixel image gauche * -0.0458 + Dose Verte pixel image gauche * -0.0484 + Dose Bleue pixel image gauche * -0.0257 + Dose Rouge pixel image droite * 0.3756 + Dose Verte pixel image droite * 0.7333 + Dose Bleue pixel image droite * 0.0111
Dose Bleue pixel anaglyphe = Dose Rouge pixel image gauche * -0.0547 + Dose Verte pixel image gauche * -0.0615 + Dose Bleue pixel image gauche * 0.0128 + Dose Rouge pixel image droite * -0.0651 + Dose Verte pixel image droite * -0.1287 + Dose Bleue pixel image droite * 1.2971
De ces équations on peut facilement comprendre que la composante rouge résultante de l’anaglyphe –gauche- est composée essentiellement des couches rouge 41% et verte 47% de l’image de gauche, un peu de la composante bleue de l’image de gauche 16%, diminuée faiblement par les composantes RVB de l’image de droite –faibles coefficients négatifs < 3%-. On remarque que la composante bleue de l’image de droite est fortement augmentée de 30% dans l’anaglyphe. La composante verte sera dépendante de la composante rouge ce qui introduit une certaine diaphotie (injection de l'image de gauche dans la droite et vice versa). Les doses RVB résultantes sont interdépendantes des doses RVB des images du couple stéréo.
| 1.0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1.0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1.0 |
c'est à dire que l'on utilise simplement la couche rouge de l'image de gauche et les couches verte et bleue de l'image de droite, sans "mélange" !
Dans "Producing anaglyphs from synthetic images", W. Sanders et David F Mc Allister donnent pour des lunettes No 7003 de www.reel3d.com + des écrans types CRT & LCD :
| 0.4561000 | 0.5004840 | 0.1763810 | -0.0434706 | -0.0879388 | -0.00155529 |
| -0.0400822 | -0.0378246 | -0.0157589 | 0.3784760 | 0.7336400 | -0.0184503 |
| -0.0152161 | -0.0205971 | -0.0054686 | -0.0721527 | -0.1129610 | 1.2264000 |
Attention !!! Plus les valeurs des coefficients de l'image homologue sont importants ET PLUS on ajoute de DIAPHOTIE qui détruit le relief dans l'anaglyphe obtenu puisqu'il y a une moins bonne séparation gauche/droite. Ces coefficients sont repérés en caractères italiques non gras dans la matrice ci-dessus. Avec des coefficients forts pour l'homologue, on peut aboutir à un résultat sans relief puisque on peut injecter autant l'image de gauche dans l'image de droite et vice versa. La matrice de transformation idéale est celle qui supprime les rivalités colorées tout en séparant bien dans l'anaglyphe final l'image de gauche et l'image de droite -non diaphotive-, en préservant au mieux les couleurs initiales !
Une feuille de calcul pédagogique au format Microsoft Excel 2003 est disponible ici (format Excel 2007 ici). Dans cette feuille Excel vous entrez les doses RVB des couleurs des pixels homologues dans l'image de gauche et l'image de droite pour obtenir celle de l'anaglyphe. Cette feuille calcule aussi les coordonnées CIE XYZ, xyz de la couleur obtenue dans le diagramme colorimétrique CIE de 1931.
Le diagramme de la commission internationale de l'éclairage CIE est une représentation de l'ensemble des couleurs observables par une personne "standard", un œil humain standard. L'ensemble des couleurs monochromatiques sont représentées par une courbe graduée de 380nm à 700nm, un morceau du spectre, c'est le spectrum locus. Toutes les autres couleurs ne sont pas monochromatiques, le blanc est le mélange de toutes les couleurs en synthèse additive. Le blanc est représenté aux coordonnées xy(0.33,0.33) dans ce diagramme. Un des intérêts de cette représentation est le fait que si l'on sélectionne trois couleurs primaires sur ce graphique, alors les couleurs dérivées possibles synthétisables seront inscrites dans le triangle dont les sommets sont ces couleurs primaires. Les sources des luminophores des écrans sont dans ce cas. Donc avec un écran, vous ne pouvez pas recréer toutes les couleurs observables dans la nature...
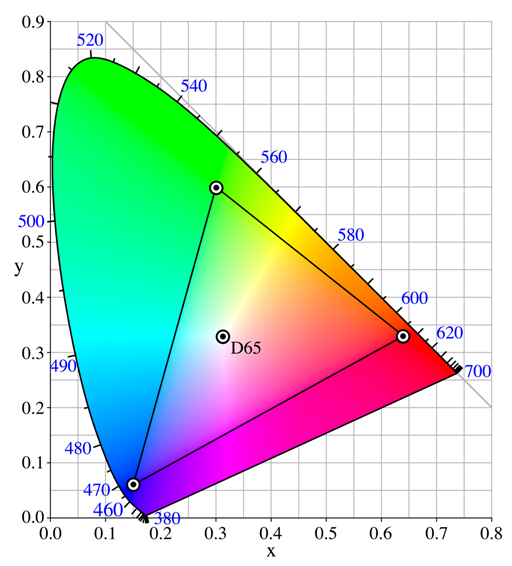
Wikipedia : Diagramme CIE
Il illustre parfaitement l'espace théorique des couleurs qu'il est possible de percevoir en omettant les effets de basse luminance (qui font apparaître des teintes rabattues comme le marron). L'ensemble des couleurs spectrales (i.e. les couleurs des lumières monochromatiques - ou des diverses longueurs d'onde du visible) est représenté sur le diagramme par cette courbe en forme de fer à cheval graduée de 380 à 700 nm, le "spectrum locus" ou lieu du spectre visible.
Analysons quelques résultats numériques pour comprendre facilement cette transformation :
Ainsi un objet rouge pur dans une scène d'anaglyphe RVB(255,0,0) à la position CIE xy(0.73,0.26) dans le diagramme colorimétrique CIE est transformé dans l'anaglyphe en un jaune orangé faible RVB(103,84,0) à la position CIE xy(0.46,0.52). Il est "seuillé" car il perd 0.6 fois son flux initial dans le rouge (et donc l'image de gauche). La transformation lui ajoute 84 unités de vert (dans l'image de droite). Le rapport de flux œil gauche/œil droit qui était énorme avec la couleur originale 255/(0+0) est maintenant de (103/84) = 1,22. Ce rouge qui ne passait que dans l’œil gauche passe maintenant dans les deux yeux mais n’est plus vraiment rouge. Ce rouge est maintenant adapté au procédé anaglyptique. Il est plus stéréoscopique. Cette transformation fera disparaître des rouges forts au profit du jaune-orangé ou jaune-vert. Un rouge vif parait donc moins lumineux dans un anaglyphe et plus marron. Un point d'échelle unitaire -pixel- de cette couleur est situable en profondeur sans ambigüité car elle peut porter la parallaxe sans aucune ambigüité.
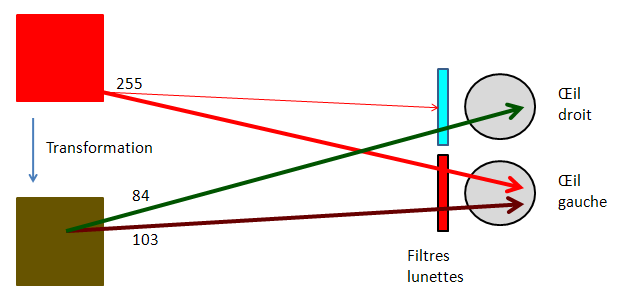
Illustration de la transformation d'un objet rouge pur par méthode Dubois : Le rouge pur ne passe que dans le filtre rouge, il est absorbé par le filtre cyan, il ne parvient pas à l'œil droit.
Où situer un détail de la taille unitaire -d'un pixel- isolé sur un fond blanc et d'une couleur perçue par un seul œil ?
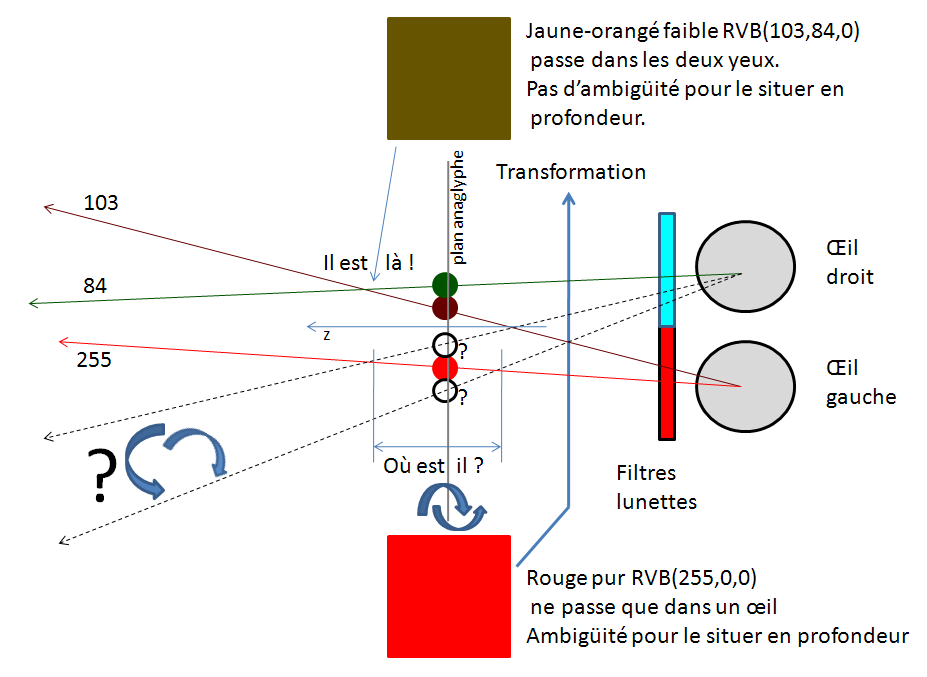
Illustration de la transformation de la couleur d'un détail unitaire -pixel- rouge pur par méthode Dubois et sa situation en profondeur : Le rouge pur ne parvient pas à l'œil droit donc le cerveau n'a pas l'information de parallaxe et ne peut le situer dans l'espace, il hésite avec l'interprétation cérébrale, le cerveau cherche l'information de l'œil droit autour mais la situation dans l'espace varie... Le cerveau peut s'aider des formes et contours des objets sur l'anaglyphe mais ce n'est pas forcément suffisant. La couleur obtenue par transformation du rouge pur parvient au deux yeux. A l'échelle du pixel, le cerveau obtient donc une information de parallaxe, il peut situer le pixel dans l'espace sans ambigüité.
On pourrait croire que le transport de la profondeur et du relief dans un anaglyphe s'effectue uniquement par l'analyse cérébrale des bordures et contours des objets dans les images de gauche et de droite mais ce n'est pas suffisant. Comme nous l'avons souligné au début de cette page pédagogique, il y a toute une gradation dans le problème de rivalités colorées. Une couleur ne vibre pas d'un coup, ce n'est pas binaire mais progressif. Une couleur est donc plus ou moins adaptée graduellement au transport de l'information de la profondeur et va donc plus ou moins détruire les nuances de relief dans l'anaglyphe. Ainsi dans les deux illustrations qui suivent, vous ne percevez pas les disques et cercles à la même profondeur alors que la parallaxe est IDENTIQUE pour chaque ligne. ATTENTION, POUR BIEN VOIR CES NUANCES IL FAUT VOUS PLACER DANS LES CONDITIONS OPTIMALES DE VISUALISATION, c'est à dire un écran bien réglé en luminosité et être dans une ambiance plutôt sombre pour ne pas détruire le contraste de l'écran. Un anaglyphe idéal est donc celui qui dispose de "couleurs stéréoscopiques" qui ne détruisent pas les nuances de relief...
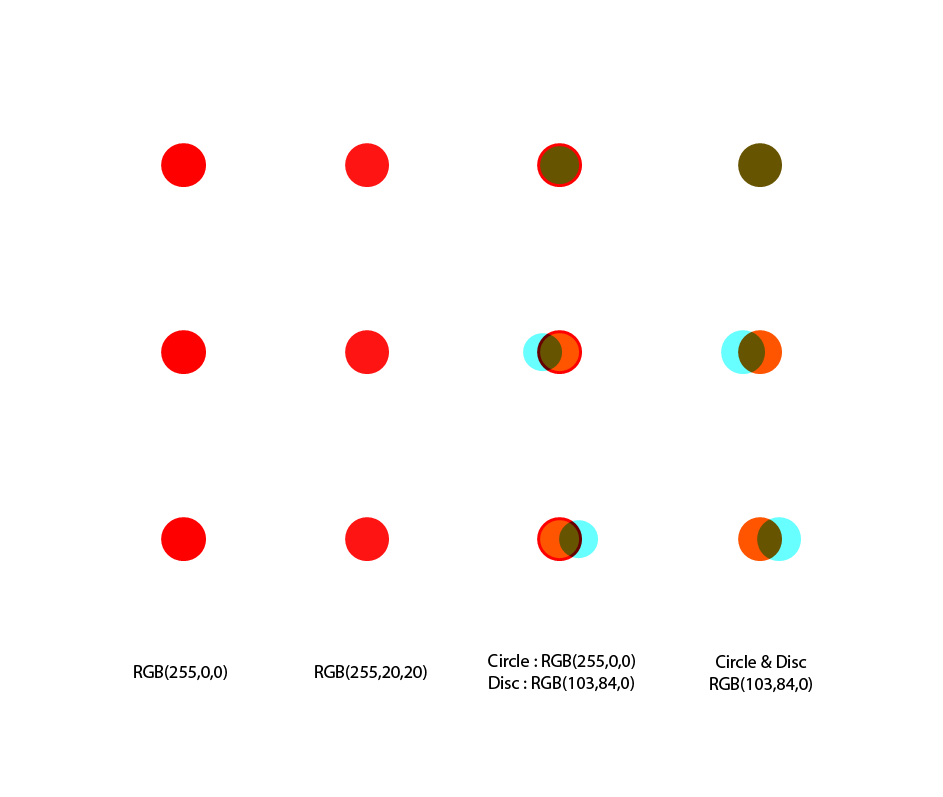
Illustration du transport du relief dans un anaglyphe : On pourrait croire que la profondeur est uniquement transportée par le décalage parallactique des bordures, contours et limites des objets dans les deux images gauche et droite. C'est plus compliqué qu'il n'y parait. Dans l'illustration ci-dessus, les bordures/limites des formes sont visibles par les deux yeux (masquez alternativement l'un des deux filtres des lunettes pour vérifier les bonnes conditions d'observation). Mais sur chaque ligne, vous ne devez pas situer les deux colonnes les plus à droite à la même profondeur malgré un décalage horizontal de parallaxe identique. Les deux dernières lignes ont un décalage en sens inverse. Seule la profondeur de la colonne la plus à droite est perceptible correctement. La forme de la deuxième colonne la plus à droite contient un disque de la même couleur (un rouge pur transformé via LS Dubois) mais elle est entourée d'un cercle rouge pur (Circle & Disc). La conséquence visuelle est évidente, cette colonne n'est pas vue à la même profondeur que la plus à droite alors qu'elle le devrait ! La couleur rouge pure dont la forme est visible car le disque est de plus grand diamètre dans la couche rouge provoque une gêne et perturbe la bonne situation en profondeur.
Liens vers les couches R, V et B de cette illustration.
Prenons le cas d’un objet cyan RVB(0,255,255) à la position xy(0.22,0.35), la transformation produit un bleu-gris (152,171,255) en "seuillant" le vert à 171 unités, en ajoutant 152 unités de rouge et en saturant la composante bleu à 255.
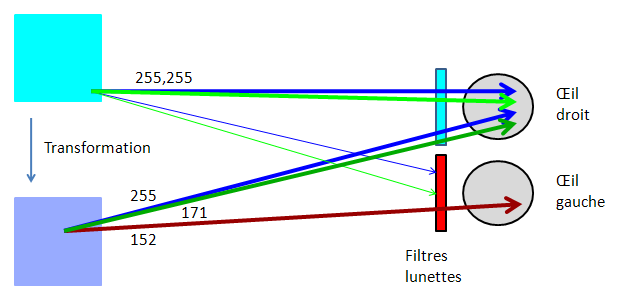
Illustration de la transformation d'un objet cyan pur par méthode Dubois.
Prenons le cas d’un objet vert pur RVB(0,255,0) à la position xy(0.27,0.71) dans le diagramme colorimétrique CIE. Ce vert est transformé en un jaune-vert RVB(111,175,0). Il est aussi "seuillé" car il passe d’un flux de 255 à 175 unités soit 0.68 fois la valeur initiale. La transformation lui ajoute 111 unités de rouge. Idem que pour le rouge pur, l’objet vert pur est maintenant d’une couleur qui passe dans les deux yeux. Le cerveau peut bien le situer sans équivoque à l'échelle du point unitaire dans l’axe de la profondeur.
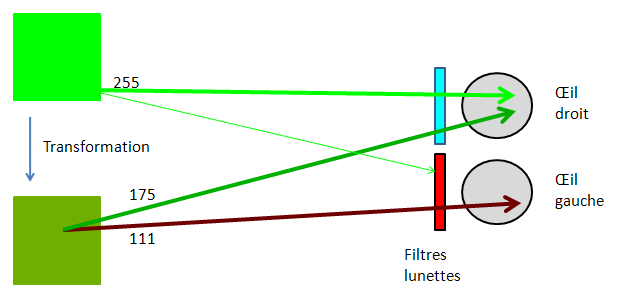
Illustration de la transformation d'un objet vert pur par méthode Dubois.
Pour le bleu pur RVB(0,0,255) à la position xy(0.16,0.0) la transformation produit un bleu avec une petite quantité de rouge RVB(41,0,255). C'est-à-dire que là aussi la transformation ajoute du rouge dans le deuxième œil.
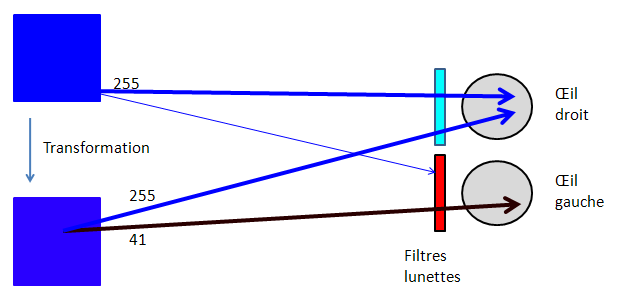
Illustration de la transformation d'un objet bleu pur par méthode Dubois.
Le blanc RVB(255,255,255) est quant à lui toujours blanc après cette transformation. Il conserve son flux initial, il n’est pas transformé en gris (blanc moins lumineux).
Nous avions présenté des illustrations sur les rivalités colorées au début de cette page pédagogique. Voici ces mêmes illustrations mais dont les couleurs ont été transformées par la méthode d'Eric DUBOIS. L'action de répartition est évidente sur la teinte rouge qui n'apparait plus à l'état pure :
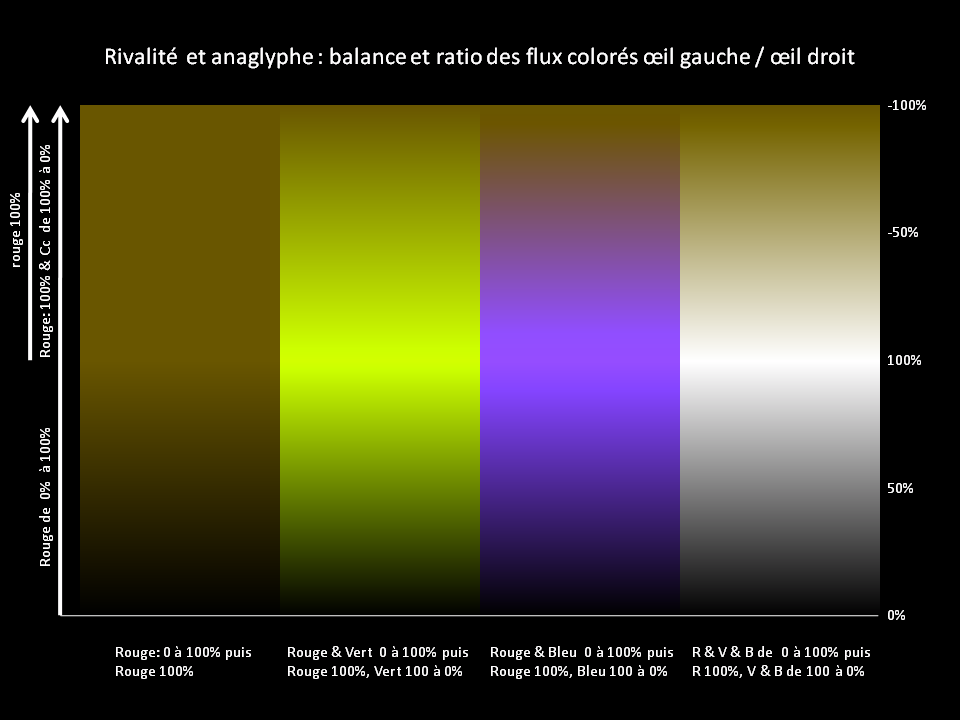
Variations sur les nuances de ROUGE maxi -œil gauche - TRANSFORMEES par la méthode Dubois
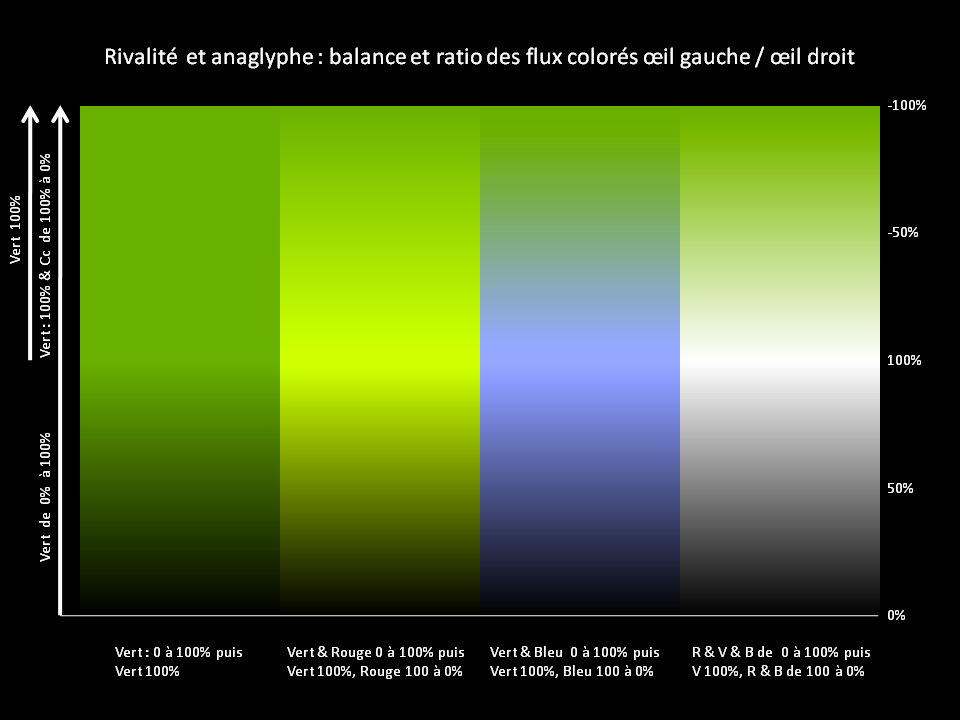
Variations sur les nuances de VERT maxi -œil droit - TRANSFORMEES par la méthode Dubois
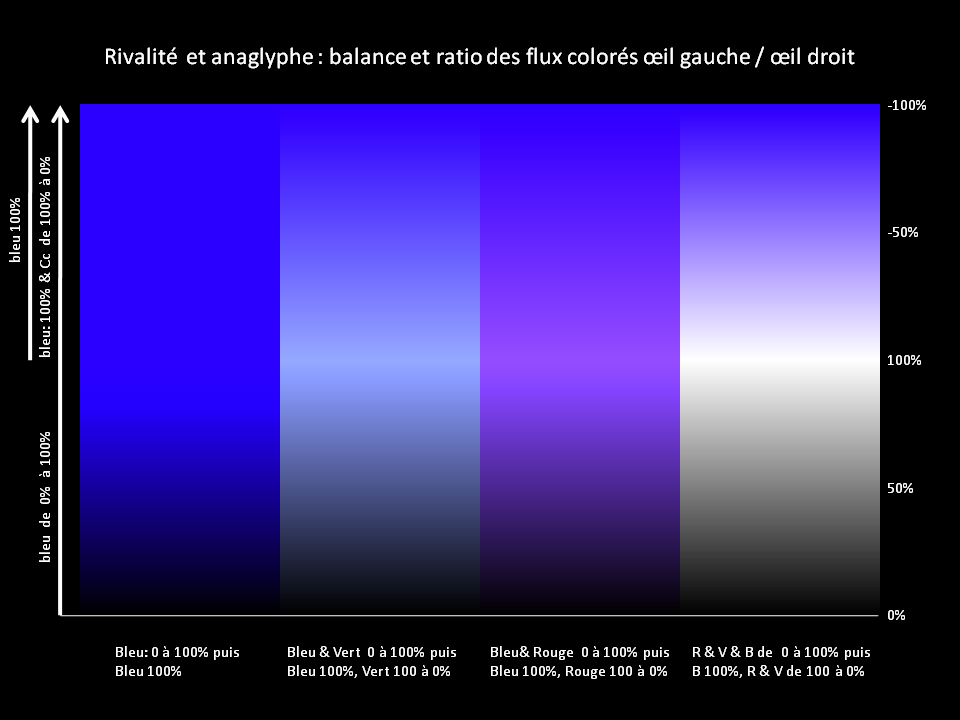
Variations sur les nuances de BLEU maxi -œil droit - TRANSFORMEES par la méthode Dubois
Analysons maintenant la transformation d'un ensemble de couleurs :