Géométrie de la prise de vue stéréoscopique :
Dans l"illustration ci-dessous, on schématise la géométrie d'une prise de vue stéréoscopique (avec 1 ou 2 appareils, en même temps ou en deux temps) impliquant des objets (A, B, C). Ces objets sont plus ou moins distant des optiques du photographe (aux distances DA, DB, DC), et du capteur lumineux (ou la rétine d'un observateur). On se place dans une situation simple et pédagogique où les objets A, B, C sont parfaitement alignés :
- A est l'objet le plus lointain ou à l'infini (les montagnes au loin dans l'illustration en anaglyphe sur la droite) ;
- B est un objet proche des appareils photographiques ou des yeux (pieds de bruyère) ;
- C est un objet très proche et même trop proche qui ne satisfait donc pas certaines conditions.
Les objectifs photographiques (ou le cristallin des yeux) sont symbolisés sur le bas par des ellipses grises et transparentes (la valeur de la focale de cette lentille est f). Les capteurs lumineux où se forme l'image (CCD, CMOS, film, rétine) sont symbolisés par des rectangles noirs.
La distance entre les appareils pour les deux prises de vues à t0 et t1, soit la base stéréoscopique ou encore la dispartié binoculaire (distance entre les yeux) est de valeur b.
Les rayons lumineux qui passent par le centre optique des objectifs ne sont pas déviés. Il est alors très simple d'en déduire où les images se forment sur les capteurs :
- pour l'objectif de gauche (ou l'oeil gauche), ou encore la première photographie au temps t0 (si on procéde en deux temps avec un seul appareil) : les images des points A, B et C sur le capteur sont confondues en un point O car ils sont parfaitement alignés ;
- pour l'objectif de droite (ou l'oeil droit), ou encore la deuxième photographie au temps t1 : l'image du point A se forme en A'' sur le capteur, l'image du point B se forme en B'' et l'image du point C se forme en dehors de la surface du capteur (car trop petit) en C''.
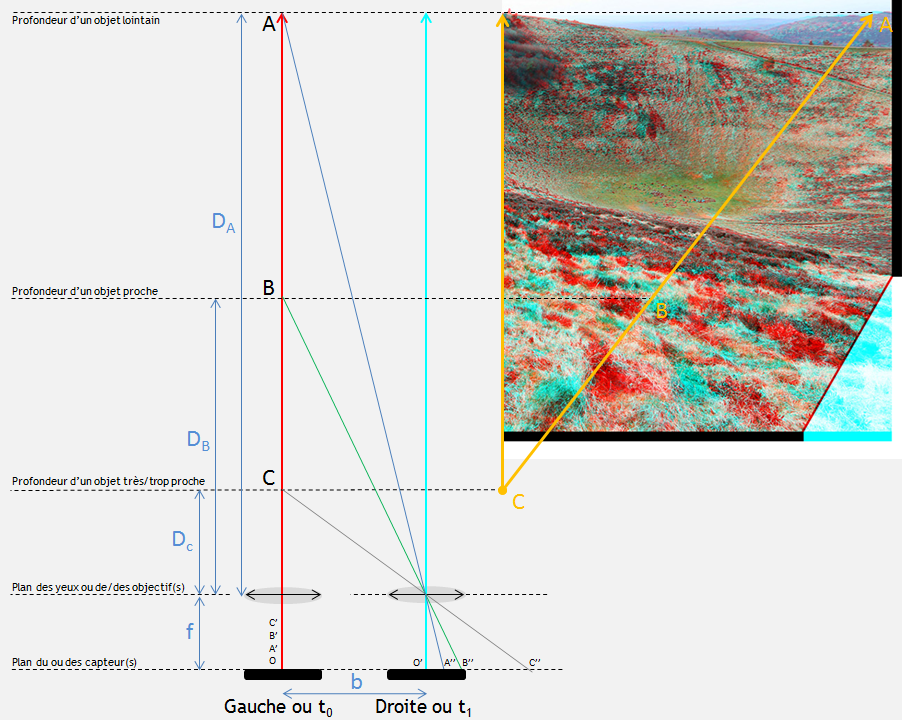
Illustration 1 : Géométrie lors de la prise de vue stéréoscopique. Muni de lunettes anaglyptiques, vous constaterez que l'illustration comporte une énorme violation de fenêtre sur le bord gauche de la partie image. La violation de fenêtre est une faute de montage stéréoscopique qu'il faut éviter car on place le cerveau dans une situation qui n'est pas naturelle. Cette violation de fenêtre est corrigée par une découpe de cohérence stéréoscopique sur le bord gauche.
L'angle OCC'' est la parallaxe que représente la base stéréoscopique depuis le point C.
L'angle OBB'' est la parallaxe que représente la base stéréoscopique depuis le point B le plus proche.
L'angle OAA'' est la parallaxe que représente la base stéréoscopique depuis le point le plus éloigné A.
Les distances O'A'', O'B'' et O'C'' sont respectivement les écarts de parallaxe projetés sur le capteur des objets A, B et C. On remarque par cette illustration que plus l'objet est lointain, plus l'écart de parallaxe projeté est faible sur le capteur. Pour un objet à l'infini, il est théoriquement nul.
Les relations géométriques de Thalès dans le triangle permettent d'écrire que pour l'objet proche B situé à une distance DB de l'objectif dont l'image se forme sur le capteur droit en B'' avec un écart parallactique de valeur O'B'' :
(1) 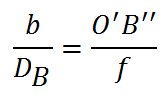 , soit dans le cas général :
, soit dans le cas général :
(2) 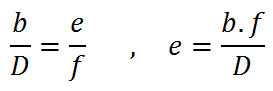 , où D est la distance de l'objet à l'objectif, e l'écart de parallaxe sur le capteur, f la focale, b la base stéréoscopique.
, où D est la distance de l'objet à l'objectif, e l'écart de parallaxe sur le capteur, f la focale, b la base stéréoscopique.
Le stéréophotographe doit toujours adapter la base en fonction de la scène et l'objet au premier plan lors de la prise des vues. Il est donc intéressant d'exprimer la base à utiliser en fonction de l'écart maximal qu'il souhaite sur le capteur, entre les positions de l'image du point le plus proche et celui du plus lointain. C'est à dire en fonction de la distance A''B'' = O'B'' - O'A'' qui va donner la "force/quantité" du relief au stéréocliché. Pour une même dimension restituée du document stéréophotographique, plus cette dimension sera grande et plus le relief sera fort, plus cette dimension sera petite et plus le document semblera plat et sans relief (mais il y a des limites physiologiques) :
(3) 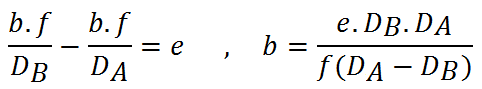 cette formule est fondamentale en stéréoscopie.
cette formule est fondamentale en stéréoscopie.
Dans l'exemple de l'illustration 1, on a DA=583 pixels, DB=297 pixels, f=76 pixels, e=18 pixels (environ). La base doit donc être de b = (18.2*297*583)/(76*(583-297)) = 145 pixels.
Dans cet exemple pédagogique, la base b représente une parallaxe au point B de tan(p) = b / DB = 145 / 297 soit p = 26°. Cette valeur est énorme pour le cerveau et pas du tout une valeur tolérable de confort physiologique. Cette dernière équation est purement géométrique et ne tient pas compte de notre physiologie, il peut être intéressant de la contraindre avec ce que le cerveau trouve confortable durant une conférence ou une suite de projection stéréoscopique, sans déformation de la profondeur de l'image, avec un écart parallactique e constant.
La valeur de confort parallactique est comprise entre 1,1° et 4° CAR ELLE DEPEND DE LA DIMENSION DE RESTITUTION DU DOCUMENT FINAL (on utilisera plutôt 1° pour un écran de cinéma, et entre 2 et 3° pour un moniteur informatique). La valeur commune de 1,9° dans la bibliographie correspond à l'écartement de nos yeux de 65 mm pour un objet situé à 2 m de nous. C'est la règle historique des 1/30 utilisée pour du film 36 mm avec un objectif de focale 35 mm, ce qui provoque un écart paralactique de 1,2 mm sur le film, soit 3,4 % de la largeur du film et donc 3,4 % de l'image restituée lors d'une projection si l'opérateur n'a pas retaillé l'image capturée.
Pour une même dimension de restitution du document : sans ou pas assez de parallaxe, le relief est plat. Avec trop de parallaxe, le document n'est pas confortable voir détestable pour le cerveau, en dehors de ces limites, les objets sont alors déformés. Il peut donc être intéressant de rechercher la distance minimale DB de manière à obtenir une parallaxe de confort pc que l'on juge intéressante pour un type de document : On pose que tan pc = b / DB et donc b = DB tan pc que l'on injecte dans (3). Après quelques lignes d'équations, on obtient une équation du second degré qui admet une seule solution puisque l'une des racines est toujours nulle (si le centre optique et l'objet sont confondus ;-) ! ). ATTENTION : Ces formules vous fournissent une distance théorique exacte en fonction des autres paramètres, les résultats peuvent surprendre et ne pas être pratiques pour la prise de vue. On perçoit déjà que tout est affaire de compromis en stéréophotographie. En pratique, on fera souvent varier la parallaxe (entre des limites raisonnables) pour la prise des vues car DA, f sont des fixes, et on cherchera plutôt à conserver e dans la série des clichés pour que les spectateurs n'aient pas à réaccomoder leur vision, faire de fréquentes rotations des yeux entre les clichés. L'exercice n'est pas simple en pratique pour le photographe :
.(4) Distance de confort au premier plan 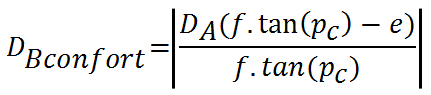 avec une base de confort :
avec une base de confort :
(5) Base stéréoscopique de confort 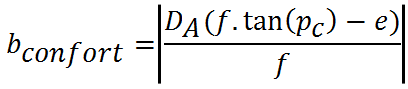
- DA est la distance en mm de l'objet le plus loin A dans le champ stéréophotographique ;
- DB confort est la distance en mm de l'objet le plus proche B dans le champ stéréophotographique pour obtenir la parallaxe de confort ;
- f est la vraie focale de l'objectif en mm ;
- pc est la parallaxe de confort en radians vue depuis l'objet le plus proche B dans le document stéréoscopique (généralement entre 1° et 4°, souvent 2°) ;
- e est l'écart en mm entre les parallaxes projetées sur le capteur des points les plus proches et les plus lointains dans le document stéréoscopique ;
- bconfort est la base stéréoscopique à utiliser pour obtenir une parallaxe pc depuis l'objet le plus proche B.
Il est intéressant d'exprimer e (l'écart maximal des parallaxes projetées sur le capteur) comme une fraction de la dimension du capteur utilisé (généralement dans les 1 à 5 %). En fait, nous verrons que pour le confort de l'observateur, ce pourcentage dépend de la dimension de l'écran de projection utilisé et du placement des spectateurs pour la diffusion des documents stéréoscopiques.
Illustration 2 : Influence de la parallaxe de la prise de vue. Les ballons de Rugby et de football sont pris à 2 m de distance avec un Canon G11 (f=6.1 mm). DA, DB et f sont fixes mais les bases stéréoscopiques de gauche à droite sont de 120 mm, 200 mm et 300 mm. La parallaxe de prise de vue est donc respectivement de 3,4° - 5,7° et 8,5° ce qui implique que l'écart e du point le plus lointain (la paille au fond) varie sur le capteur et donc sur ces documents restitués. La limite de confort visuel est franchie dèjà à partir de 5,7°, la plus à droite est désagréable pour le cerveau alors qu'elle est fusionnable sur le plan des écarts des homologues qui ne dépasse pas la distance entre nos deux yeux sur le moniteur. Elle déforme les objets, le ballon de foot n'est plus sphérique.
Une autre illustration de 2,3° à 13,5° est disponible ici (largeur 400 pixels) et ici (largeur 800 pixels).
RESTITUTION : À quelle distance du spectateur se forme le volume du document stéréoscopique ? Profondeur de fusion des points homologues ? Calcul de la distance du spectateur au relief fusionné stéréoreproduit :
Un observateur situe la profondeur d'un point A à l'intersection des deux segments qui partent des ses yeux et passent par les points homologues affichés sur l'écran (point A dans l'image de droite, même point A dans l'image de gauche). L'illustration 3 schématise la profondeur obtenue pour 3 points particuliers A, B et C.
Sur la gauche, on trouve la tête du spectateur et ses deux yeux espacés d'une disparité binoculaire d'eip mm. Au centre, le rectangle noir symbolise l'écran de projection (ou moniteur informatique) sur lequel les deux images du couple stéréoscopique sont affichées, supperposées. On utilise le rouge pour l'image correspondante à l'oeil gauche, le cyan pour l'image destinée à l'oeil droit. Le sens et l'écart sur l'écran entre les points homologues rouge-cyan détermine le lieu où le point sera fusionné et situé par l'observateur dans le sens de la profondeur. Le point A est fusioné en avant de l'écran à une distance Dfp de l'observateur. Le point B est fusioné derrière l'écran à une distance Dfl de l'observateur. Le point C est fusioné sur la surface de l'écran puisque l'écart entre ses points homologues est nul. Si l'écart des homologues est égal à celui des yeux alors l'objet est fusioné à l'infini très très loin derrière l'écran (effectivement lorsque nous regardons l'horizon au loin nos yeux s'orientent parallèles). On peut facilement calculer la profondeur de fusion des homologues ou la distance entre les yeux du spectateur et le point stéréoreproduit, par la formule :
(6) 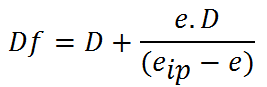 où Df est la distance des yeux de l'observateur où sont fusionés les deux homologues en mm, D la distance des yeux de l'observateur à l'écran de projection en mm, eip est l'écart inter pupilaire (65 mm pour l'adulte, 45 mm pour l'enfant), e est l'écart en mm entre les deux homologues sur l'écran de projection ( valeur e > 0 si l'homologue droit est bien à droite dans ce cas le point sera situé derrière l'écran de projection, e < 0 dans ce cas le point sera situé devant l'écran en jaillissement par l'observateur).
où Df est la distance des yeux de l'observateur où sont fusionés les deux homologues en mm, D la distance des yeux de l'observateur à l'écran de projection en mm, eip est l'écart inter pupilaire (65 mm pour l'adulte, 45 mm pour l'enfant), e est l'écart en mm entre les deux homologues sur l'écran de projection ( valeur e > 0 si l'homologue droit est bien à droite dans ce cas le point sera situé derrière l'écran de projection, e < 0 dans ce cas le point sera situé devant l'écran en jaillissement par l'observateur).
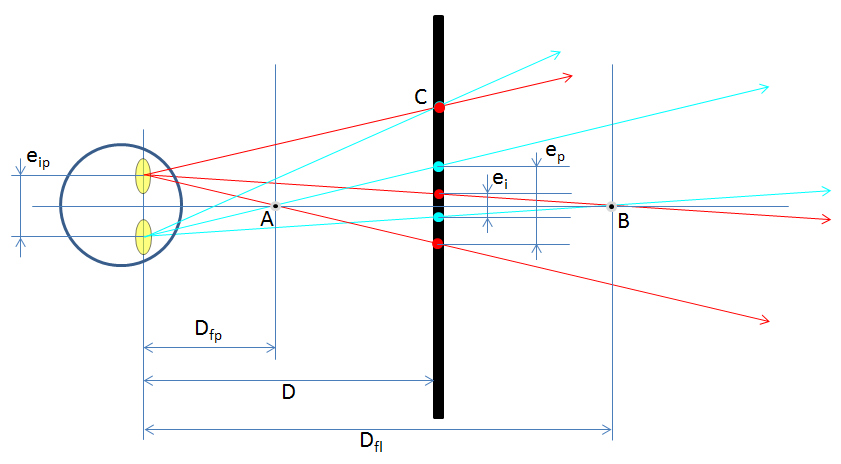
Illustration 3 : Profondeur de la fusion des homologues. Lieu où le cerveau situe un point en fonction de l'écart des homologues sur l'écran de projection. ei est l'écart des homologues sur l'écran de projection du point B le plus lointain de la scène stéréoreproduite (on parle souvent de l'écart des infinis). ep est l'écart des homologues sur l'écran de projection du point A, le plus proche de l'observateur de la scène stéréoreproduite, en jaillissement dans cet exemple.
Nos yeux ne peuvent que très peu diverger, pour le confort d'observation on ne doit pas faire diverger nos yeux pour les infinis :
L'illustration ci-dessous schématise la divergence oculaire (dpo , ou ddo) que subissent deux spectateurs lors d'une projection stéréoscopique sur écran (respectivement au premier rang distant de Dpo et au dernier rang distant de Ddo). Ces observateurs ont un même écart inter pupilaire eip. Ils observent un document stéréoscopique dont les points homologues (droit, gauche) pour l'infini (ou objet le plus lointain dans la scène) représentent un écart einf sur l'écran de projection. L'observateur le plus proche subit forcément la divergence la plus grande. Il y a divergence oculaire lorsque l'écart des infinis est plus grande que la disparité binoculaire des observateurs (il serait donc logique de travailler pour la disparité des enfants 45-50 mm). Notre système musculaire osculateur permet une divergence de 1° maximum. Seuls les stéréoscopistes habitués peuvent fusionner le relief avec une telle divergence des yeux. 0,5° est déjà une limite pour la plupart d'entre nous.
Dans le cas idéal, il convient de ne pas placer les spectateurs dans cette situation. On fera en sorte que l'ensemble prise de vue (base) - projection (réglage) produise un écart des infinis inférieur à la distance inter pupilaire commune, c'est à dire 65 mm (pour les adultes) et 45 mm (pour les enfants). En fait, ces valeurs ne sont atteintes que sur de grands écrans, dans des grandes salles ou sur des TV 3D de grandes dimensions.
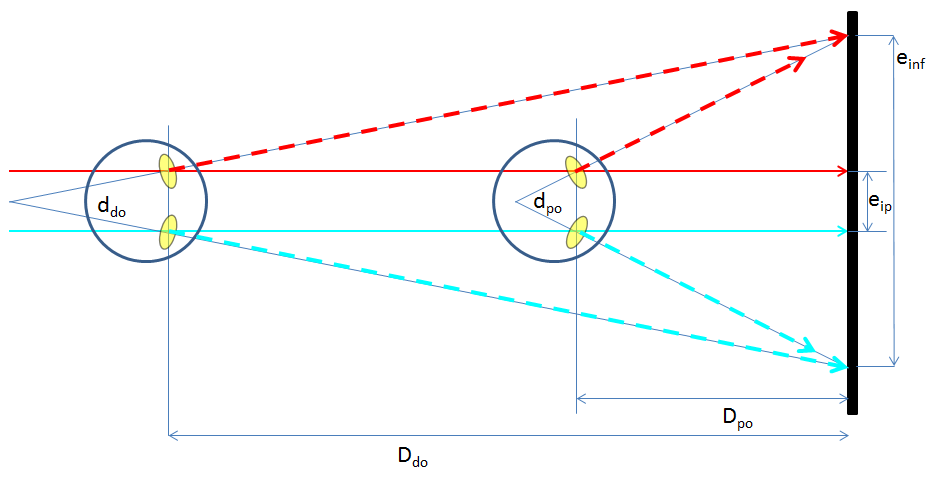
Illustration 4 : Schématisation de la divergence oculaire de deux spectateurs identiques observant les infinis (ou objet le plus loin dans la scène stéréoscopique, dont les homologues provoquent l'écart le plus important sur l'écran de projection).
La divergence des infinis de la scène stéréoreproduite peut être calculée par la formule suivante :
(7) 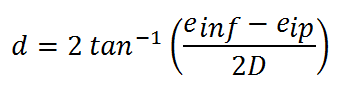 où d est la divergence en degrès DOIT ETRE INFERIEURE << à 1° , et conseillée plutôt < à 0,5°, einf est l'écart en mm des homologues pour les infinis (ou objet le plus lointain de la scène), eip est l'écart inter pupilaire en mm pour le public considéré, D est la distance en mm entre le spectateur et l'écran. Par exemple pour un adulte situé à 2 m de l'écran, si l'écart des homologues pour l'infini est de 71 mm, la divergence oculaire du spectateur est d = 2*tan-1((71-65)/(2*2000)) = 0,17° ce qui est une valeur encore acceptable pour l'homme mais pas conseillée, à éviter.
où d est la divergence en degrès DOIT ETRE INFERIEURE << à 1° , et conseillée plutôt < à 0,5°, einf est l'écart en mm des homologues pour les infinis (ou objet le plus lointain de la scène), eip est l'écart inter pupilaire en mm pour le public considéré, D est la distance en mm entre le spectateur et l'écran. Par exemple pour un adulte situé à 2 m de l'écran, si l'écart des homologues pour l'infini est de 71 mm, la divergence oculaire du spectateur est d = 2*tan-1((71-65)/(2*2000)) = 0,17° ce qui est une valeur encore acceptable pour l'homme mais pas conseillée, à éviter.
Zone de tolérance de fusion du relief :
Lorsque nous fixons un point M à une distance D, seul un ensemble d'objet situés dans un petit volume autour du point M sont vus simples (non dédoublés sans diplopie physiologique). Fixez la feuille centrale d'un arbuste ou d'une plante pour vous en persuader. Les feuilles centrales fixées sont nettes et on perçoit bien le relief, les feuilles périphériques sont floues voire dédoublées si vous êtes trop proche.
Le système cérébral admet donc une aire de tolérance autour du point M projeté sur la rétine pour la vision simple des objets (vision non dédoublée). Cette aire dont la dimension varie avec la zone physique sur nos rétines, est appelée l'aire fusionnelle de Panum (Ludvig Peter 1820-1885). Sa forme est ovaloïde avec son grand axe dans le sens horizontal. La correspondance rétinienne ne se fait donc pas point à point (situés physiquement au même endroit sur les rétines respectives) mais aires à aires (donc avec une tolèrance).
L'aire spatiale de Panum est la région de l'espace où les objets sont vus simples (sans diplopie) dans le champ de vision stéréoscopique binoculaire. Elle définie la zone de vision stéréoscopique.
L'illustration ci dessous représente la forme et l'étendue de l'aire spatiale de Panum obtenue par la méthode dite "haplopic" pour un point de fixation situé à 40 cm, droit devant l'observateur (tige fixe en F, tige amovible en profondeur). La graduation horizontale représente l'écart angulaire au point de fixation F. L'axe vertical représente la distance en mm sur la profondeur. La zone contenant le plan dit de l'horoptère h, bordée par les limites de l'ensemble des points bleus et rouges, est la zone où la tige (amovible sur l'axe de la profondeur) est perçue simple tout en fixant le regard sur la tige fixe en F. C'est la zone de vision binoculaire simple. En dehors de la limite externe bleue et la limite interne rouge, elle est perçue dédoublée. C'est la zone de diplopie physiologique.
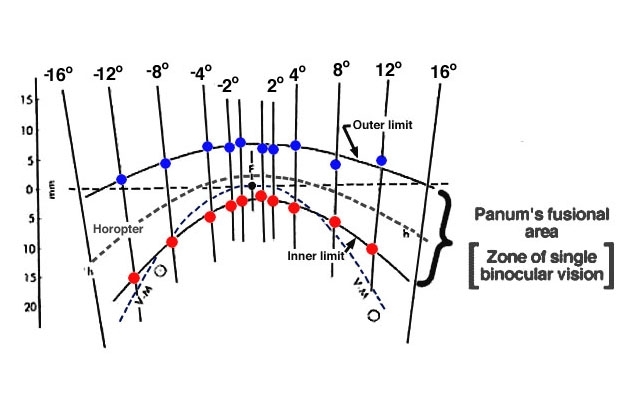
Illustration 5 : Les dimensions de l'aire spatiale fusionnelle de Panum obtenues par la méthode haplopic pour un point fixé F à 40 cm. Expérience de Moses RA & Hart WM (1987) dans Adler's Physiology of the eye, Clinical Application, 8th ed, St. Louis. V-M est le cercle de Vieth-Muller ou horptère théorique géométrique. h est l'horoptère longitudinal réel.
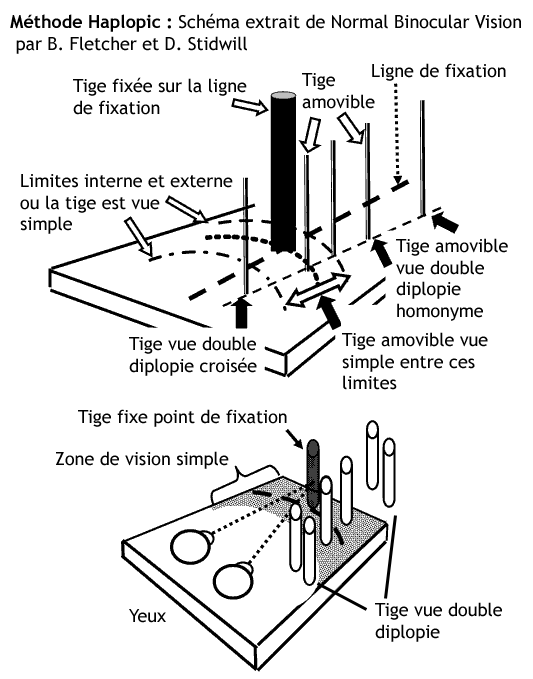
Illustration 6 : Instrumentation de mesure par la méthode Haplopic, tige amovible en profondeur et tige fixe pour mener l'expérience de Moses RA & Hart WM (1987). Crédit : Normal binocular vision, B. FLETCHER & D. STIDWILL.
Le problème est identique lorsque nous observons un document stéréoscopique. Les limites physiologiques sont à priori les mêmes. Il faut placer le spectateur dans une situation où il pourra fusionner les points homologues de toute la scène stéréoreproduite en fixant l'axe du sujet d'intérêt (point de fixation M) sans avoir trop à accommoder sur les différentes profondeurs/plans du document (changer la profondeur du point fixé M).
Sauf à observer un petit document stéréoscopique, l'observateur devra toujours déplacer ses yeux sur l'objet d'intérêt dans le document (notament sur les bords) pour l'aligner avec sa fovéa sur sa rétine. La fovéa est la zone du maximum d'acuité visuelle (sur 3 à 5°). Idéalement, il faut donc que la profondeur de relief globale du document stéréoscopique dans l'axe soit contenue dans l'aire spatiale de Panum vue à la distance D idéale d'observation du document, et particulièrement pour des objets proches et lointains qui se recouvrent.
En reprenant l'illustration 3 et en lui ajoutant une représentation des limites approchées de l'aire spatiale de Panum (verdâte) passant par les point A (point le plus proche de l'observateur dans le volume virtuel stéréoreproduit) et B (point le plus loin de l'observateur dans le document stéréoscopique), on peut rechercher la distance d'observation idéale pour le confort du spectateur. Il faut que les angles αf = (A,Ga,B) et (A,Dr,B) soit inférieurs à une valeur de confort. Pour ma part, j'utilise une valeur de confort de 0,3° mais on peut dépasser cette valeur.
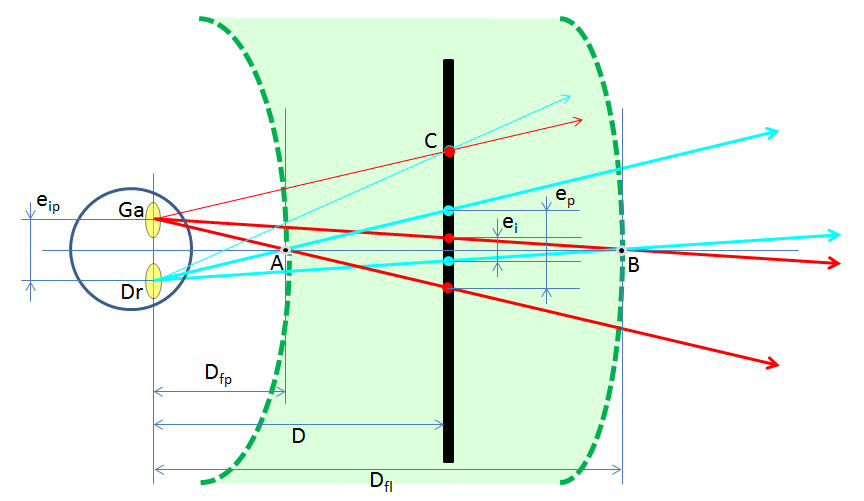
Illustration 7 : Recherche de la distance idéale d'observation D d'un document stéréoreproduit pour satisfaire à la profondeur de l'aire spatiale de Panum du spectateur, dans l'axe d'observation, entre les objets les plus proches et plus lointains qui peuvent de recouvrir (illustration 5). C est confondu avec l'écran, A est en jaillissement, B est fusioné loin derrière l''écran. Les angles (A,Ga,B) et (A,Dr,B) sont égaux.
eip est l'écart en mm entre les deux yeux ;
ei est l'écart en mm du point le plus loin du spectateur du document stéréoscopique (dit des infinis). Par convention, e > 0 s'il est fusionné derrière l'écran ;
ep est l'écart en mm du point le plus proche du spectateur. e = 0 s'il est confondu avec l'écran de projection. Par convention, e < 0 s'il est en jaillissement de l'écran, fusionné entre l'observateur et l'écran ;
D est la distance en mm de l'observateur à l'écran de projection ou le document stéréoscopique ;
Dfp est la distance en mm de l'observateur au point A fusionné le plus proche à l'avant plan dans le volume stéréoreproduit, idéalement dans le volume de Panum ;
Dfl est la distance en mm de l'observateur au point B fusionné le plus loin au fond du volume stéréoreproduit, idéalement dans le volume de Panum ;
αf = (A,Ga,B) et (A,Dr,B) dans Illustration 7, est l'angle de fusion entre les objets les plus proches et les plus lointains de la scène stéréoreproduite, dans la direction du regard de l'observateur, autour du sujet d'intérêt.
On obtient l'angle de fusion global du volume stéréoreproduit αf = (A,Ga,B) = (A,Dr,B) par la formule :
(8) 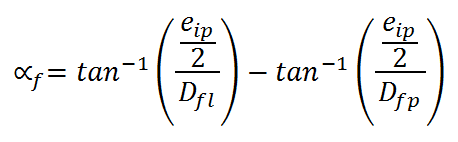 , que l'on peut écrire en fonction de D en injectant dans (8) l'expression de Dfl et Dfp de (9) :
, que l'on peut écrire en fonction de D en injectant dans (8) l'expression de Dfl et Dfp de (9) :
(9) 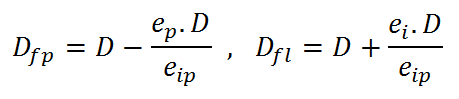
Il est intéressant de connaître la distance idéale où doit se positionner l'observateur pour que l'ensemble de la scène stéréoreproduite soit une partie raisonnable de son volume de Panum axial sans dépasser ou même toucher ses limites. On cherche donc à exprimer D en fonction de l'angle de fusion de l'ensemble de la scène αf , dans l'axe l'observation (j'utilise 0.3°comme valeur de confort). Après la réduction des équations (8) et (9), on obtient la solution par la résolution d'une équation du second degré ou D est l'inconnu (11) :
(10) On pose z : 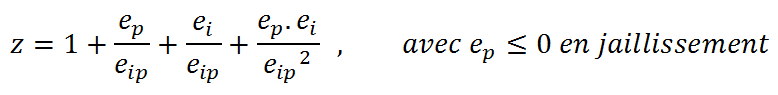
(11) 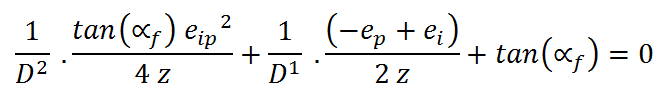
la solution pour D est dans (12) :
(12) 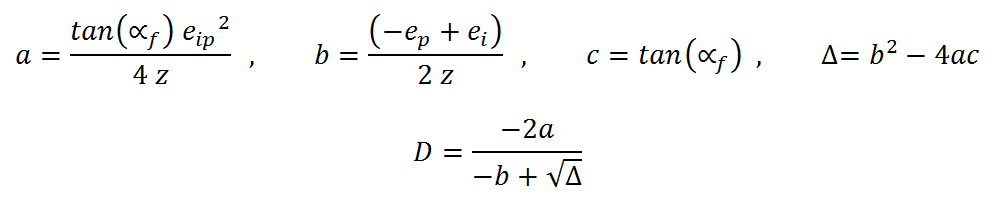
Notes physiologiques sur la fusion de la vision binoculaire :
La fusion du relief n'est pas parfaitement possible sur le volume entier du champ de vision. Lorsqu'un observateur fixe un point à une distance D, ses yeux convergent vers ce point d'intérêt M, il est vu simple, non dédoublé. Cet observateur voit net et non dédoublé dans un volume autour de cette position (en profondeur et latéralement). Ce volume est d'autant plus grand que l'observateur regarde loin (signe d'une tolérance angulaire), la plage angulaire de fusion correcte du relief représente à cette distance un volume de plus en plus important autour du point d'intérêt. En revanche, cette zone se réduit avec la proximité de l'objet. Vous pouvez faire cette expérience en observant le feuillage fourni d'un arbuste ou d'une plante plus ou moins proche de vous.
Dans un cas extrême, si un observateur fixe par exemple un ballon moderne de Rugby situé à 1 m de lui avec le sens oblongue vertical. La totalité du ballon lui apparait avec son relief bien perceptible simple et non dédoublé, les micros picots à la surface de la partie centrale sont bien nets sur environ 7 cm de diamètre, zone où l'acuité visuelle est la meilleure (sur 3 à 5°).
Si l'observateur introduit son doigt par la droite dans le champ visuel (à une distance de 20 cm des yeux, tout en conservant son acuité sur le ballon), il percevra d'abord un seul doigt car il n'est visible que par un oeil (champ de 60° du côté nasal et 90° du côté temporal ce qui induit un champ binoculaire d'environ 120° avec deux champs monoculaires temporaux de 40-50°).
Lorsque ce doigt est perceptible par les deux yeux, il voit 2 doigts flous.
Deux problèmes se mèlent : la mise au point optique de l'oeil et la diplopie = pas de fusion des deux images, l'objet est perçu dédoublé. Le doigt est dédoublé car le cerveau ne peut pas fusionner ses deux images obtenues dans chaque oeil. Comparé entre chaque rétine, l'image obtenue pour ce doigt est trop distante du ballon, pas dans la tolérance cérébrale. Le problème est identique si l'on remarque un objet bien en arrière du ballon. La diplopie admet deux seuils en profondeur.
On parle de diplopie croisée lorsque les lignes de regard se coupent en arrière du point d'intérêt (objet est vu double avant la limite), ou homonyme lorsque les lignes de regard se coupent en avant (objet est double après la limite).
L'ensemble des points vus simples lorsque l'observateur fixe un point M est appelé l'horoptère. L'horoptère est le lieu de l'espace où les objets sont vus simples tous à la fois. C'est le cercle théorique passant par le point M et le centre optique des yeux de l'observateur. Il s'agit d'une vision restrictive théorique concentré sur un point de l"espace M et ne tenant pas compte des seuils de la diplopie dont nous avons parlé ci-dessus. Comme la diplopie admet les seuils croisés et homonymes dans le sens de la profondeur (Illustration 6), tous les points de la zone entre ces seuils sont vus simples et non dédoublés. Un point est perçu simple si ses images rétiniennes se forment sur les aires de Panum.
Quelques définitions utiles liées à l'oeil et la vision :
- Vision simultanée = perception comme une image unique de deux images strictement différentes percues chacune par un oeil dans une même direction. C'est le 1er degré de la vision binoculaire ;
- Fusion = perception comme image unique de deux images qui ne différent l'une de l'autre que par quelques détails. C'est le 2e degré de la vision binoculaire ;
- Macula = région centrale de la rétine proche de l'axe optique de l'oeil. Cette région (2 mm) dispose d'une importante concentration de cônes. Elle est aussi appelée la tache jaune. Elle contient la fovéa ;
- Fovéa = région centrale de la macula de la rétine où se concentrent les cônes pour une acuité maximale dans le prolongement de l'axe optique de l'oeil ;
- Horoptère géométrique théorique = Le centre de l'horoptère géomètrique est le point de fixation. C'est un plan circulaire qui passe par le centre optique des yeux et le point de fixation (cercle de Vieth-Muller). Il s'agit d'un plan de l'espace dont chaque point se projette sur un couple de points rétiniens équidistants de leur fovéa respective. La correspondance rétinienne se fait rigoureusement point à point ;
- Horoptère longitudinal = c'est l'ensemble des points de l'espace se projettant sur des points rétiniens non correspondants (pas au même endroit sur les deux rétines) le long du méridien horizontal et passant par la fovéa. Ils ne sont pas équidistants de la fovéa comme pour l'horoptère géométrique. Ce n'est donc pas un cercle ;
- Horoptère vertical = ensemble des points de l'espace contenant les objets situés à égale distance des yeux et se projetant sur des points rétiniens correspondants le long du méridien vertical et passant par la fovéa ;
- Diplopie = perception dédoublée d'un objet ;
- Confusion = mauvaise localisation d'un objet dans l'espace ;
- Aire spatiale de Panum = zone de l'espace visuel située de part et d'autre de l'horoptère longitudinal et au niveau de laquelle les points sont vus simples (non dédoublés, sans diplopie). Elle a la forme d'une lentille biconcave ;
- Aire fusionnelle de Panum = c'est l'aire spatiale de Panum projetée sur la rétine. C'est une aire sur la rétine où la vision est unique (non dédoublée) alors que l'image ne se forme pas sur deux points correspondants de la rétine dans chaque oeil. Sa forme est ovale avec un plus grand diamètre horizontal. C'est une zone de tolérance. Sa surface dépend de la nature du stimulus visuel, de la localisation sur la rétine. La surface est réduite sur la macula et augmente si on s'éloigne de la fovéa, vers la périphérie de l'oeil ;
- Diplopie physiologique = diplopie des objets en avant ou en arrière de l'aire spatiale de Panum (ou du point de fixation) qui se projettent sur des points rétiniens-aires rétiennes fusionnelles non correspondantes ;
- Diplopie croisée = vision dédoublée des objets situés en avant de l'aire spatiale de Panum et qui se projettent dans le secteur temporal de la rétine ;
- Diplopie homonyme = vision dédoublée des objets situés en arrière de l'aire spatiale de Panum et qui se projettent dans le secteur nasal de l'aire fusionnelle de Panum sur la rétine ;
Limiter l'effet de pixelisation, résolution de l'oeil :
Il faut placer le spectateur de manière à ce qu'il ne puisse distinguer les plus petits éléments constituant l'image (grains ou pixels). Dans le cas d'une projection numérique, on placera l'observateur de manière à ce qu'il ne percoive pas l'effet d'escalier des pixels, la pixellisation de l'image. Dans le cas d'une projection argentique, on le placera de manière à ce qu'il ne percoive pas le grain de la diapositive. On pourrait se baser sur le pouvoir de résolution de l'oeil de 1' d'angle (= 1/60°) mais ce critère est beaucoup trop simpliste car les effets de contraste interviennent. On obtient la dimension angulaire que représente un élément d'image numérique par :
(13) 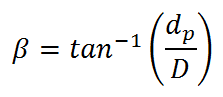 où dp est la dimension du pixel carré en mm, D est la distance de l'observateur en mm. Il faut multiplier β par 60 pour obtenir la valeur en minutes de degré '/°.
où dp est la dimension du pixel carré en mm, D est la distance de l'observateur en mm. Il faut multiplier β par 60 pour obtenir la valeur en minutes de degré '/°.
Conclusion :
Tous les éléments géométriques et physiologiques nécessaire à la prise de vue et à la restitution d'un document stéréophotographique en relief sont détaillés dans cette page. La bibliographie se limite souvent aux aspects géométriques. J'ai voulu introduire au maximum les éléments de confort visuel pour les spectateurs. Le stéréophotographe méticuleux pourra calculer sa prise de vue en fonction des paramètres et du média de restitution prévu. Il faut souvent tatonner entre les différentes variables, se placer plus proche, s'éloigner, accepter le compromis. J'ai programmé toutes ces formules dans une feuille Excel. Les paramètres sont placés sur le haut de la feuille de calcul, les résultats intéressants pour le stéréophotographe à la suite. Voici quelques exemples pré remplis pour :
- la prise de vue et la diffusion d'une scène dont le premier objet est situé à 30 m du photographe, l'objet le plus lointain à 40 km. Le stéréophotographe réalise les clichés au zoom 27 (affiché par Stereo Data Maker SDM). Il souhaite une parallaxe différentielle de 3% de la taille du capteur. Il diffusera le résultat sur une TV 3D LG 47LW5500 de 47 pouces de diagonale soit 1040 mm dans le sens horizontal pour 1920 pixels. La distance idéale d'observation pour un angle de confort de 0,3° est de 2 m - Feuille Excel ;
