
COMPLEMENTS SUR LA MISE EN STATION D'UNE MONTURE EQUATORIALE (1/3)

Trajectoire réfractée d'un astre
Luc DETTWILLER - Michel GOUTTESOLARD - Alain MAURY - David ROMEUF - 1992
Article paru en trois volets dans les numeros 695 (Mars-Avril 1993), 696 et 697 de la revue PULSAR de la SAP

L'objet de cet article est de rappeler la méthode photographique de mise en station publiée par l'astronome américain E.S.King, de proposer au lecteur une variante visuelle testée par les auteurs, et enfin, de présenter une méthode de compensation des dérives d'astres induites par la réfraction atmosphérique.
SOMMAIRE
C - Variante visuelle à la méthode de KING
1 - Connaître l'action des vis calantes
2 - Contrôle de la vitesse d'entraînement
3 - Centrage dans l'oculaire réticulé de n'importe quelle étoile du champ polaire et attente de la dérive éventuelle
Figure 6 : Une carte du pôle boréal
D - Conclusion générale et synthèse
A - Influence de la réfraction atmosphèrique
I - Importance de la mise en station
La mise en station d'une monture équatoriale est primordiale pour la qualité des travaux que réalisera le manipulateur. Cette action consiste simplement à rendre parallèle l'axe de rotation de la monture à celui de la Terre afin de compenser facilement la rotation de celle-ci par un seul moteur entraîné à vitesse constante (but: image observée immobile); le rayon terrestre étant négligeable dans la plupart des cas devant la distance des astres observés.
En effet, si l'axe de rotation de la monture n'est pas parfaitement parallèle à l'axe de rotation de la Terre alors il sera impossible de suivre un astre sans correction. Ceci se concrétisera par une dérive de l'astre dans le champ oculaire (ou photographique) malgré une vitesse de rotation précise du télescope : 1 tour en 23h 56m 4.09s [1]; ou alors, par une rotation du champ oculaire (ou photographique) autour d'une étoile que l'on poursuivrait à l'oculaire réticulé en agissant sur les commandes du télescope. La vitesse d'un point du champ variant alors avec la distance de l'étoile guide il vaut mieux prendre une étoile présente sur le cliché et "idéalement" en son centre.
Concrètement et en exagérant, le défaut de mise en station sera surtout gênant en astrophotographie car on ne pourra jamais avoir d'étoiles "ponctuelles" (pour une résolution donnée du négatif) mis à part celle que l'on aura suivie ! Le phénomène s'accentue avec le champ et la focale de l'instrument.
Il existe pratiquement une bonne dizaine de méthodes permettant de mettre en station un télescope. Elles différent toutes quant à leur efficacité et leur précision. Certaines permettent de caler le télescope sans que le pôle céleste soit visible ou pointable (ex: BIGOURDAN). La plus précise (quelques secondes d'arc en théorie) est celle de KING décrite plus loin.
Rappelons ici la méthode de Bigourdan Elle consiste à voir la dérive au cours du temps d'un astre au méridien (calage du pôle sur l'horizontale) puis celle d'un astre au lever ou coucher (calage du pôle en hauteur). Le processus est itératif, mais la pratique démontre que le procédé demande parfois d'assez longs tâtonnements [2], et, est limité intrinsèquement par la réfraction atmosphérique (voir ci-dessous). Sa longueur fait aussi que le manipulateur, de guerre lasse, se contente souvent de peaufiner uniquement la dérive méridienne.
La solution pour obtenir de belles photographies n'est pas non plus d'acheter ou construire une CCD d'autoguidage sans mettre l'instrument en station. Ce matériel pourtant excellent ne pourra pas faire grand chose contre la rotation du champ. Il permettra par contre un bon guidage. La mise en station est donc toujours une des bases de la technique instrumentale dont on ne peut se passer.
[1] Rappelons que c'est le jour sidéral qui nous intéresse ici, et non pas le jour solaire moyen de 24 heures : un astre fixe passe au méridien local tous les 23h 56mn 4.09s.
[2] Voir "LUNETTES ET TELESCOPES de Dangeon et Couder (page 358 à 361).
II - Analyse de la trajectoire diurne d'un astre
Dire que la trajectoire diurne d'un astre fixe est un arc de cercle est un peu simpliste car on oublie manifestement la réfraction atmosphérique !
1 - La réfraction atmosphérique :
L'optique géométrique nous enseigne qu'un rayon lumineux est dévié lorsqu'il traverse un milieu d'indice de réfraction variable, tournant sa concavité en direction des indices croissants. Notre brave atmosphère n'échappe pas à cette loi physique et même complique un peu les choses car l'indice de réfraction (le pouvoir de dévier les rayons) varie avec l'altitude à cause de sa température, de sa pression et de sa composition qui ne sont pas homogènes. On a alors un gradient d'indice de réfraction, l'indice augmentant en général lorsqu'on se rapproche du sol. Concrètement un rayon lumineux qui se propage de manière rectiligne dans le vide est dévié progressivement au fur et à mesure qu'il pénètre dans l'atmosphère, en tournant sa concavité vers le sol (figure 1). De ce fait la direction apparente de l'astre observé n'est pas la direction vraie.
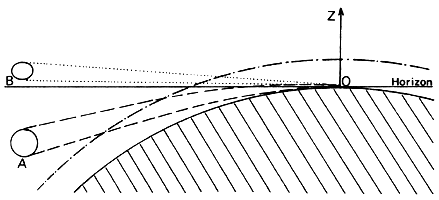
Figure 1 - La réfraction atmosphérique : Les rayons lumineux provenant du vide et entrant dans l'atmosphère sont déviés dans le sens des indices de réfraction croissants. L'angle AOB est l'angle de réfraction dirigée vers le zénith pour le bord inférieur du Soleil ou de la Lune. Le bord supérieur ne subissant pas la même réfraction, le Soleil ou la Lune nous paraissent "aplatis".
Pour un observateur la réfraction atmosphérique se manifeste par une élévation vers le zénith (la verticale du lieu d'observation) de la direction apparente de l'astre; il n'y a aucune déviation dans le sens horizontal, c'est à dire en azimut (si on considère que l'indice en un point ne varie, avec la position de ce point, qu'en fonction de son altitude). De sorte que l'on voit toujours un astre plus haut qu'il ne l'est véritablement.
Cette élévation mesurable par un angle r (appelé angle de réfraction atmosphérique) s'accroît avec la distance angulaire du zénith à l'astre (distance zénithale z). Cet angle de réfraction est nul au zénith, de 1' (minute de degrés : 1 /60) à 45° de hauteur apparente au-dessus de l'horizon, et, d'environ 36' (supérieur au diamètre apparent du Soleil et de la Lune) à l'horizon. De plus il ne varie pas de manière linéaire avec la distance zénithale mais approximativement en tan z si z est inférieure à 75°. A son lever et coucher, on observe donc le Soleil en forme de ballon de rugby alors qu'il est géométriquement couché. Ajoutons que les valeurs ci-dessus varient légèrement avec la pression, la température (elles sont ici pour 0° C et 1000 mb), et la longueur d'onde considérée. Ceci entraîne une irisation de l'image d'un astre dans le sens vertical. L'image rouge est plus proche de l'horizon, l'image bleue est plus proche du zénith. On peut observer le phénomène sur des images planétaires (bord de l'anneau de Saturne actuellement, quand elle est proche de l'horizon).


Illustration 1 : Couché de Soleil déformé par la réfraction athmosphèrique : Image de Stéphane ANGLARET (Association des Astronomes Amateurs d'Auvergne A.A.A.A) sur la terrasse de l'Observatoire du Pic du Midi. Lunette de 60 mm.
2 - Trajectoire réfractée d'un astre
Du fait de la réfraction atmosphérique, la trajectoire apparente diurne d'un astre n'est jamais un arc de cercle puisque ces rayons lumineux ne subissent pas la même déviation au cours de sa visibilité. La déformation de la trajectoire apparente de l'astre due à la réfraction dépend beaucoup de sa déclinaison et de la latitude du lieu d'observation (figure 2 et 2 bis).
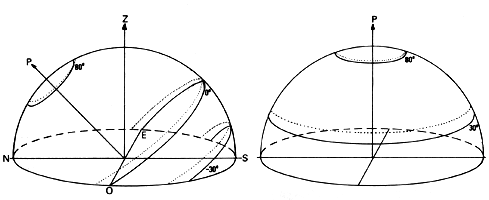
Figure 2 (à gauche) - Trajectoire réfractées (en pointillés) d'astres de différentes déclinaisons et pour un lieu d'observation de latitude 45°. La valeur de la réfraction a été exagérée sur le graphique pour des besoins de compréhension.
Figure 2 bis (à droite) Trajectoire réfractées de différentes déclinaisons pour un observateur situé au pôle Nord. Les formes des trajectoires sont totalement différentes de celles de la figure 2. Ici, l'astre décrit un arc de cercle plus haut que sa position vraie. Ces trajectoires apparentes varient donc avec la latitude du lieu pour une même déclinaison.
Dès lors, pour nos latitudes et pour certaines déclinaisons, la poursuite "en aveugle" ne pourra se faire avec un simple moteur malgré une monture mécaniquement parfaite et, parfaitement en station ! Un astre se levant subit une réfraction qui diminue dans le temps (non de manière linéaire et sur les deux axes horaires et de déclinaison) au fur et à mesure qu'il approche de son passage supérieur au méridien. Puis le phénomène s'inverse lorsqu'il passe le méridien et va se coucher. On le voit donc plus longtemps qu'on ne le devrait d'environ deux minutes au lever et au coucher. Cette brave réfraction nous donne donc environ 4 minutes de Soleil en plus ! (cette valeur dépend de la déclinaison de l'astre).
A nos latitudes la réfraction induit une vitesse qui s'ajoute à la vitesse sidérale sur les deux axes (horaire et de déclinaison) et de plus varie avec l'angle horaire. La vitesse de poursuite sur l'axe horaire est alors maximale au passage méridien, minimale au lever ou coucher. Le moteur horaire doit donc accélérer puis décélérer. Considérons que l'on vise la direction apparente d'un astre de déclinaison nulle, à son lever, et que l'axe de la monture est parallèle à l'axe terrestre. Alors dans le champ de l'instrument il semblera dériver sur l'axe de déclinaison vers le Sud céleste au lever, vers le Nord céleste au coucher et n'aura aucune dérive instantanée au méridien (au coucher le mouvement diurne tend à le faire descendre vers l'horizon dans le temps alors que la réfraction l'élève de plus en plus; il va donc de plus en plus vers le Nord céleste qu'il ne le devrait). Dans certains cas, le mouvement propre de l'astre (mobile, ex: comète) suivi peut être de même amplitude que le mouvement induit par la réfraction.
En résumé on peut dire qu'un astre n'a pas la même vitesse au cours de sa visibilité à cause de la réfraction. Si on veut éviter des corrections pour le poursuivre il faudra motoriser les deux axes de la monture et contrôler la vitesse des moteurs en fonction de son angle horaire avec comme premier postulat une monture parfaitement en station et comme deuxième une mécanique parfaite (flexion, entraînement). Si les deux conditions précédentes sont satisfaites, il est alors pratiquement possible de se passer de guidage. Mais on se heurtera sans doute a des problèmes financiers et techniques car la mise en oeuvre de moteurs et de leur contrôle en temps réel n'est pas simple pour tout le monde.
Cette conclusion invalide aussi totalement la méthode de Bigourdan pour une mise en station d'excellente qualité, en rapport à un matériel donné. Après quelques itérations (pôle instrumental à mieux que la minute d'arc du pôle céleste), on commence à suivre l'étoile pendant un temps assez long, typiquement 20 à 30 minutes. Or à nos latitudes et pour une étoile de déclinaison nulle située au méridien, la réfraction change en une demi-heure de moins de 1", ce qui est négligeable. On pourrait en théorie s'affranchir des effets de la réfraction en procédant symétriquement par rapport au passage au méridien (commencer par exemple 15 minutes avant le méridien et vérifier exactement 15 minutes plus tard) mais il n'existe pas de solution pour les étoiles pointées à 6 heures du méridien (au coucher) où la dérive due à la réfraction peut dépasser 20". La même dérive est en plus de sens contraire pour une étoile à 18 heures (au lever). La dérive observée à l'oculaire sera en fait la somme des problèmes (réfraction + défaut de mise en station + ...). Si les problèmes se compensent, on peut donc observer une étoile immobile alors qu'il y a bien un défaut de station ! Une méthode bien plus rapide et au moins aussi précise consiste à pointer directement sur le pôle, ou sur l'étoile polaire (grâce à un réticule adapté) comme il est souvent fait aujourd'hui dans un bon nombre de montures made in Japan. Une méthode du même ordre consiste à aligner directement le télescope sur son pôle instrumental. On l'équipe pour cela d'un oculaire à faible grossissement et on regarde le champ tout en tournant de plusieurs dizaines de degrés le télescope en ascension droite. Au fur et à mesure que l'on se rapproche du pôle instrumental (en réglant la déclinaison) la trajectoire apparente des étoiles s'incurve, jusqu'à tourner autour du centre du champ. Si en se déplaçant en déclinaison, on semble passer "à côté" du point où les étoiles tournent, c'est simplement que les deux axes de votre télescope ne sont pas rigoureusement perpendiculaires (cas fréquent avec les télescopes démontables). Une fois le calage réalisé on bloque les deux axes du télescope et on pointe le pôle céleste en ne déplaçant le télescope qu'en hauteur et en azimut en s'aidant par exemple de la carte de la figure 6. On réalise ainsi et en quelques minutes ce qui aurait demandé quelques heures avec la méthode de BIGOURDAN. Si l'on souhaite une plus grande précision, il faudra approfondir les problèmes théoriques.
3 - Ajustement sur le p?le réfracté d'un champ de déclinaison donnée
En déclinaison, on pourra éviter tout ce matériel complexe (moteurs et calculateur), et se contenter d'une vis judicieusement placée sur la monture pour une visée au voisinage du méridien (utile dans le cas de l'astrophotographie). La figure 3 montre pour cet exemple qu'au voisinage du méridien la trajectoire réfractée est quasiment celle que suivrait une monture ayant son pôle un peu plus haut que le pôle céleste; on parle alors du pôle réfracté d'un champ. Mais la trajectoire apparente rigoureuse de l'astre n'est plus un cercle centré sur le pôle réfracté (qui en plus se déplace lorsque l'astre s'éloigne du méridien).
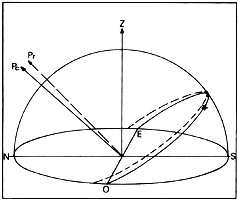
Figure 3 - Cet exemple montre bien que la trajectoire réfractée n'admet pas le même axe de rotation que celui de la Terre. En approximation, et au voisinage du méridien, on peut dire que le champ de déclinaison considéré admet un axe de rotation réfractée (pôle réfractée du champ, Pr) un peu plus haut vers le zénith que celui de la Terre (Pc).
Cette vis aura donc pour fonction de faire basculer d'un certain angle l'axe polaire de l'instrument dans le plan méridien. Il faudra veiller à modifier en conséquence la vitesse de poursuite sur l'axe horaire. Ainsi on donnera à l'instrument le mouvement qui "colle le mieux" au mouvement apparent d'un astre de déclinaison donnée, au voisinage de son passage au méridien (on pourrait faire de même pour compenser le mouvement propre de la Lune). Mais comme ce mouvement choisi pour l'instrument dépend de la déclinaison, la poursuite de tous les astres d'un champ ne pourra en théorie être parfaite puisqu'ils ont des déclinaisons différentes; en astrophotographie ceci ne sera sensible que pour des grands champs proches de l'horizon (voir dans le tableau 1 l'évolution des paramètres en fonction de h, hauteur de l'astre a son passage au méridien variant entre 15 et 25°). La réfraction différentielle qui aplatit l'image dans le sens vertical (14" sur 6° à 45° de hauteur, 73" soit 1' 13" sur 6° à 20° de hauteur), provoque alors elle même une distorsion du champ pendant la pose photo car la hauteur de chaque astre du champ varie et donc la réfraction qu'ils subissent aussi. C'est ainsi que la plupart de tous les grands télescopes de Schmidt sont pourvus d'un système permettant de modifier la hauteur du pôle instrumental afin de se caler au mieux sur le pôle réfracté de la déclinaison du champ photographié. Pour des instruments avec un champ plus faible, ou une focale plus courte, les problèmes sont évidemment bien moins sensibles.
|
Déclinaison en degrés
|
Hauteur au méridien en degrés
|
Réfraction en minutes d'arcs
|
Angle en minutes d'arcs dont on doit relever la monture vers le zénith par rapport à l'axe de rotation vrai de la Terre
|
Idem mais par rapport au pôle céleste refracté
|
Facteur de correction relatif de la vitesse de poursuite
|
Vitesse de poursuite en "/s
|
| -30 |
15 |
3.97 |
7.94 |
6.87 |
-0.002309 |
15.00634 |
| -25 |
20 |
2.92 |
4.55 |
3.48 |
-0.001322 |
15.02118 |
| -20 |
25 |
2.28 |
2.98 |
1.91 |
-0.000866 |
15.02804 |
| -15 |
30 |
1.84 |
2.13 |
1.06 |
-0.000619 |
15.03176 |
| -10 |
35 |
1.52 |
1.62 |
0.55 |
-0.000470 |
15.03400 |
| -5 |
40 |
1.27 |
1.29 |
0.22 |
-0.000374 |
15.03544 |
| 0 |
45 |
1.06 |
1.06 |
0.00 |
-0.000309 |
15.03642 |
| 5 |
50 |
0.89 |
0.91 |
-0.16 |
-0.000264 |
15.03710 |
| 10 |
55 |
0.74 |
0.79 |
-0.27 |
-0.000231 |
15.03760 |
| 15 |
60 |
0.61 |
0.71 |
-0.35 |
-0.000206 |
15.03797 |
| 20 |
65 |
0.50 |
0.65 |
-0.42 |
-0.000188 |
15.03824 |
| 25 |
70 |
0.39 |
0.60 |
-0.46 |
-0.000175 |
15.03843 |
| 30 |
75 |
0.28 |
0.57 |
-0.49 |
-0.000166 |
15.03858 |
| 35 |
80 |
0.19 |
0.55 |
-0.52 |
-0.000159 |
15.03867 |
| 40 |
85 |
0.09 |
0.54 |
-0.53 |
-0.000156 |
15.03872 |
| 45 |
90 |
0.00 |
0.53 |
-0.53 |
-0.000155 |
15.03874 |
| 50 |
85 |
0.09 |
0.54 |
-0.53 |
-0.000156 |
15.03872 |
| 55 |
80 |
0.19 |
0.55 |
-0.52 |
-0.000159 |
15.03867 |
| 60 |
75 |
0.28 |
0.57 |
-0.49 |
-0.000166 |
15.03858 |
| 65 |
70 |
0.39 |
0.60 |
-0.46 |
-0.000175 |
15.03843 |
| 70 |
65 |
0.50 |
0.65 |
-0.42 |
-0.000188 |
15.03824 |
| 75 |
60 |
0.61 |
0.71 |
-0.35 |
-0.000206 |
15.03797 |
| 80 |
55 |
0.74 |
0.79 |
-0.27 |
-0.000231 |
15.03760 |
| 85 |
50 |
0.89 |
0.91 |
-0.16 |
-0.000264 |
15.03710 |
| 90 |
45 |
1.06 |
1.06 |
0.00 |
-0.000309 |
15.03642 |
Tableau 1 : Variations des réglages en fonction de la déclinaison de l'astre, pour les même latitude (45°), longueur d'onde (0.556 micromètres), température de 15°C et pression au sol de 1025 mb.
 Exemple de monture équatorialle de type "fer à cheval" : C'est certainement la monture la plus stable, sans trop de flexions, et bénéficiant d'une grande couronne lisse pour l'entraînement ce qui améliore la poursuite. Elle est malheureusement, sans doute, la moins simple de réalisation. La monture présentée ici est une réalisation de Michel GOUTTESOLARD, et accuse un poids total de deux tonnes. Les méthodes visuelle et photographique présentée dans cette série d'articles ont été testées entre autres sur cet instrument.
Exemple de monture équatorialle de type "fer à cheval" : C'est certainement la monture la plus stable, sans trop de flexions, et bénéficiant d'une grande couronne lisse pour l'entraînement ce qui améliore la poursuite. Elle est malheureusement, sans doute, la moins simple de réalisation. La monture présentée ici est une réalisation de Michel GOUTTESOLARD, et accuse un poids total de deux tonnes. Les méthodes visuelle et photographique présentée dans cette série d'articles ont été testées entre autres sur cet instrument.
Il semble évident que si l'on souhaite avoir le pôle instrumental à quelques secondes d'arc du pôle réfracté, celui-ci devra être équipé de vis calantes permettant cette précision. Une vis sur le pied sud de la monture permet généralement le calage en hauteur et il faudra préférer la rotation de l'ensemble de la monture en azimut par rapport à un axe vertical, ou la rotation autour du pied Sud, plutôt que de modifier l'azimut en changeant la hauteur du pied Nord-Est ou Nord-Ouest car ceci change également la hauteur. Lors de cette opération de calage, l'utilisation de jauges micrométriques au centièmes sera d'une très grande utilité.
Afin de connaître la modification de la vitesse angulaire de poursuite, et la valeur de l'angle dont on doit relever l'axe de la monture, dans le but de réaliser le mouvement de l'instrument qui "colle le mieux" au mouvement apparent d'un astre de déclinaison donnée (lors de son passage au méridien), Luc DETTWILLER a conduit un long calcul dont voici les résultats pour le passage supérieur (au passage inférieur la hauteur de l'astre est la plus faible donc il est dénué d'intérêt pratique). La précision de ces résultats est de l'ordre de 2 % pour un astre culminant à 15° de hauteur, et s'améliore rapidement quand celle-ci augmente. Un programme en langage BASIC permettra d'obtenir rapidement les valeurs numériques de ces résultats pour différents paramètres.
Soit ns l'indice de réfraction de l'air au niveau du sol, qui dépend de la température, de la pression et de la longueur d'onde ;
Soient t la température au sol en degrés Celcius, p la pression athmosphèrique au sol en mb et Lambda la longueur d'onde considérée en micromètres (0.556 est celle du maximum de sensibilité de l'oeil) ;
ns-1 = (n0-1) . (p/1013.25) / (1+0.00367.t)
où n0 est l'indice de réfraction au sol pour une température de 0°C et une pression de 1013.25 mb, donné (à 0.1% près dans le domaine visible) par :
n0-1 = 0.0002879 + 1.63e-06 / Lambda^2
Epsilon = ns -1.0 = 3.10e-04 donc trés inférieur à 1.
Soient Phi la latitude du lieu, Delta la déclinaison de l'astre et Tau le facteur de correction de la vitesse d'entraînement en valeur relative.
* Si l'axe de l'instrument est parallèle à l'axe de rotation de la Terre, il faut déplacer l'axe de la monture vers le zénith d'un angle Omega donné par :
Omega = (Epsilon.sin(2.Phi)) / (2.cos(Phi-Delta)^2)
et corriger en valeur relative la vitesse d'entraînement d'un facteur Tau :
Tau = -Epsilon.(cos(Phi)/cos(Phi-Delta))^2 = -|Omega.cotan(Phi)|
La vitesse d'entraînement sera alors :
W = Wsid.(1+Tau) (Wsid est la vitesse sidérale)
* Si l'instrument a été mis en station dans la direction du pôle céleste apparent (visée polaire, méthode de King) qui par rapport au pôle céleste est relevé vers le zénith de Epsilon.cotan(Phi), on déplacera l'axe de la monture vers le zénith d'un angle Theta :
Tetha = -Epsilon.cotan(Phi).((1-sin(Phi)^2) / (cos(Phi-Delta)^2)
La vitesse d'entraînement sera modifiée comme précédemment.
'
' CALCUL DU pôle REFRACTE D'UN CHAMP MERIDIEN (A 2% PRES SI h > 15°)
'
' (d)1992 David ROMEUF & Luc DETTWILLER
'
CLS
CLEAR
'
pi = 3.141592654#
pi2 = pi / 2
trad = pi / 180
tdeg = 180 / pi
'
' Vitesse angulaire siderale : wsid en "/s
'
wsid = 360 / (23 + 56 / 60 + 4.09 / 3600)
'
INPUT "Latitude du lieu d'observation en ° ............. :", latitude
INPUT "Temperature au sol en ° Celsius ................. :", T
INPUT "Pression atmospherique au sol en mb ............. :", p
INPUT "Longueur d'onde consideree en micrometres (0,556) :", Lambda
PRINT
INPUT "Declinaison de depart en ° :",d0
INPUT "Declinaison finale en °... :", d
INPUT "Pas du calcul en °........ :", pas
PRINT
INPUT "Impression o/n ? :", i$
IF i$ = "o" THEN i$ = "O"
'
CLS
'
' Calcul de l'indice de refraction de l'air au sol moins l'unite : ns -1
'
nsm1 = (.0002879# + 1.63E-06 / Lambda ^ 2) * (p / 1013.25) / (1 + .00367 * T)
'
PRINT
PRINT "Indice de l'air au sol - 1 ... : ns-1 ="; nsm1
PRINT
IF i$ = "O" THEN
LPRINT "Latitude du lieu d'observation :"; latitude; "°"
LPRINT "Temperature au sol ........... :"; T;" °C"
LPRINT "Pression athmospherique au sol :"; p;" mb"
LPRINT "Longueur d'onde consideree ... :"; Lambda;" micrometres"
LPRINT
LPRINT "Indice de l'air au sol - 1 ... : ns-1 ="; nsm1
LPRINT
END IF
'
latitude = latitude * trad
'
a$ = "Delta ° h ? r ' Omega ' Theta ' Tau v ""/s"
GOSUB sortie
'
FOR d = d0 TO d1 STEP pas
'
dr = d * trad
' Hauteur de l'astre a son passage au meridien
'
IF latitude > dr THEN h = pi2 - latitude + dr ELSE h = pi2 - dr + latitude
' Valeur de la refraction qu'il subit
'
r = nsm1 / TAN(h)
h = h * tdeg
' Angle dont il faut relever le monture en direction du zenith par
' rapport a l'axe de rotation de la Terre
'
Omega = nsm1 * SIN(2 * latitude) / (2 * COS(latitude - dr) ^ 2)
' Angle dont il faut relever la monture en direction du zenith par
' rapport a l'axe de rotation refracte de la Terre
'
theta = -nsm1 * (1 - SIN(latitude) ^ 2 / COS(latitude - dr) ^ 2) / TAN(latitude)
' Facteur de correction relatif de la vitesse de poursuite
'
tau = -ABS(Omega / TAN(latitude))
r = r * tdeg * 60
Omega = Omega * tdeg * 60
theta = theta * tdeg * 60
PRINT USING " ### ### ##.## ###.## ###.## ##.###### ##.##### "; d; h; r; Omega; theta; tau; (1 + tau) * wsid
IF i$ = "O" THEN LPRINT USING " ### ### ##.## ###.## ###.## ##.###### ##.##### "; d; h; r; Omega; theta; tau; (1 + tau) * wsid
NEXT d
END
'
' Sortie de a$
'
sortie:
PRINT a$
IF i$="O" THEN LPRINT a$
RETURN
|
III - Conclusion du premier volet
Avec le phénomène de réfraction qui entre en jeu (en ne pensant qu'à elle !), on se demande bien quoi faire ! Une chose est sûre, il serait préférable (au départ) de fixer le pôle instrumental sur un pôle réfracté connu et dont on peut avoir la meilleure approximation (nous saurions au moins où il est !). Pour cela il faudra éviter une méthode utilisant plusieurs champs qui ont chacun leur propre pôle réfracté, et donc se limiter à un champ unique.
En employant plusieurs champs, nous ne ferions que placer le pôle instrumental sur la "moyenne" des pôles réfractés utilisés, voir même le dernier.
 Retour au SOMMAIRE
Retour au SOMMAIRE
 Passer à la suite de l'article
Passer à la suite de l'article
 Page maintenue par David ROMEUF
Page maintenue par David ROMEUF











 Page maintenue par David ROMEUF
Page maintenue par David ROMEUF